Пусть точка U находится на расстоянии 2 от начала координат, расположена в 60° вверх от плоскости xz и на отрицательной части оси х. Следовательно, точка [/лежит в плоскости ху. Тогда точка U имеет сферические координаты (2,60°, 180°). Используя уравнение (Б.4) для пересчета точки U в декартовы координаты, получим: U- (-1, 1,732,0).
Направляющие косинусы
Направление точки U из предыдущего примера задается с помощью двух углов: широты и долготы. Часто направления задаются другим удобным способом - через направляющие косинусы. Направляющие косинусы прямой линии, проходящей через начало координат, равны косинусам трех углов, которые зта прямая составляет соответственно с осями х, у, z.
Напомним, что косинус угла между двумя единичными векторами равен их скалярному произведению. Сформируем для заданной точки [/радиус-вектор (и^ иу, иг). Длина этого вектора равна R, поэтому его следует нормировать и получить вектор единичной длины m = (ux/R, uJR, uJR). Тогда косинус угла, который этот вектор составляет с осью х, задается скалярным произведением m i = uJR, что совпадает с первым компонентом вектора т. Аналогично второй и третий компоненты вектора m являются соответственно вторым и третьим направляющим косинусом. Обозначив а, р\ у углы с осями х, у, z соответственно, получим следующие выражения для трех направляющих косинусов прямой, соединяющей 0 с точкой U:
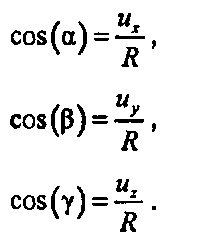
(Б.7)
Отметим, что три направляющих косинуса связаны друг с другом, поскольку сумма их квадратов всегда равна единице.
Б4. Сферические координаты и направляющие косинусы
Практические упражнения Б4.1
Преобразуйте точку (х, у, г) - (2,4, -3) в сферические координаты. Б4.2
Преобразуйте точку (г, ф, 9) - (5,35°, -67°) в декартовы координаты. Б4.3
Найдите направляющие косинусы вектора п, если О п-(1,1,1); О п = (2,3,4).
Некоторые полезные классы и служебные подпрограммы
В данном приложении описываются некоторые типы данных и алгоритмы, которые могут оказаться полезными при разработке графических приложений. Основные типы данных помещены далее в различные классы, для некоторых из этих классов даны полные описания, в то время как для других классов некоторые методы определены, но не описаны. Заполнить тела этих методов предоставляется читателю. Некоторые классы представлены только своим «скелетом», для того чтобы подсказать, как их можно было бы развить в конкретном приложении.
