(со50 + І5тф)" = С05(пф) + І5ІТі(пф).
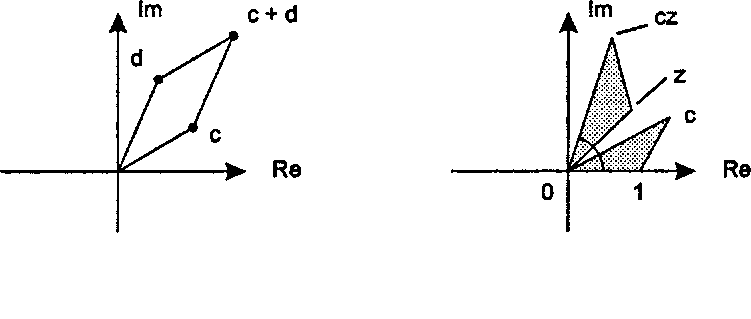
а б Рис. Б.2. Сложение и умножение комплексных чисел Исследуем более подробно функцию cos0 + fsin0. Назовем ее/(0). Из формулы Муавра следует, что /"(0) =/(пФУ возведение функции в п-ю степень эквивалентно умножению ее аргумента на п. Функция /( ) очень напоминает экспоненту и, как может быть строго доказано, действительно является ею. Это приводит нас к формуле Эйлера (Euler's formula): в'ф = COS0 + fsin0.
(Доказательство. Обе части разлагаются в бесконечные ряды с одинаковыми коэффициентами.) Отметим несколько частных случаев: е!° - 1, е'л/2 = i, еы - 1. (Последнее равенство устанавливает замечательное соотношение между четырьмя фундаментальными математическими величинами: е, i, п, 1.). Формула Эйлера предоставляет нам альтернативную и очень компактную полярную, а именно показательную форму для комплексного числа с с амплитудой |с| и углом ф: с - \с\е'ф.
Например, все п вершин и-гона радиуса R задаются п комплексными числами: pk = Reank/n, где k - 1,2,.... п.
Каждое комплексное число z имеет сопряженное (conjugate) число, обозначаемое г*. Если г = х + iy, то по определению, г* - х - iy. Тогда \z*\ = \z\ и Arg(z*) = -Arg(z). Вычисление сопряженного числа геометрически эквивалентно отражению относительно оси х. (Чему равны модуль и аргумент числа (z*)n?)
Квадратный корень Vz из комплексного числа z
Если комплексное число z имеет полярную форму z = |z| е'ф, то, очевидно, что rz=j№12.
Таким образом, квадратный корень из комплексного числа z извлекает квадратный корень из модуля этого числа и делит пополам его аргумент. Это соотношение можно написать и не пользуясь полярной формой. Если z - х + iy, то
Jz = a + ib, если у > О
Jz - -а + гЬ, если у < О, (Б.З)
' При |г| * 1 формула Муавра имеет вид: [|2|(cos0 + isin0)l" - |г|" [cos(n$) + isin(n0)]. - Примеч. пер.
Б4. Сферические координаты и направляющие косинусы
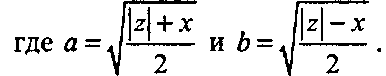
Проверка. Возведите в квадрат а + 1Ь и -а + \Ъ и после алгебраических преобразований увидите, что результат равен г.
