Пересечение трех плоскостей Пусть две плоскости пересекаются по прямой линии, а третья плоскость пересекает эту прямую в единственной точке. С помощью смешанного произведения векторов можно написать аналитическое выражение для этой точки. Если плоскости заданы уравнениями п; г = Z? , где г = 1,2,3, то их точка пересечения имеет вид:
r = fl(n2xn,)+A(n,xn,) + A(ii,xii2) ni-(n2xn3)при условии, что знаменатель отличен от нуля.
Выражение для вектора г можно проверить, убедившись, что он лежит в каждой из трех плоскостей: для этого нужно просто подставить выражение каждой плоскости в формулу для г и для доказательства равенства использовать свойства смешанного произведения.
Полезное тождество для векторных произведений При исследовании векторов, нормальных к поверхностям, приходится иметь дело с векторным произведением двух преобразованных трехмерных векторов, то есть (Ma) х (Mb), где а и b - трехмерные векторы, а М - матрица размерностью три на три. Вопрос заключается в том, как выразить это Приложение Б. Немного математики для компьютерной графики векторное произведение через векторное произведение а х Ь исходных векторов а и Ь. Это выражение имеет вид:
(Ма) х (МЬ) - (АегМ) М-Г(а х Ь), так что а х Ь масштабируется определителем матрицы М и умножается на обратную транспонированную матрицу от М. Для вывода этого результата можно проделать следующие шаги (может быть, вам удастся найти более быстрый вывод?).
Обозначьте строки матрицы М векторами г,, г2, г3. Сначала покажите, что
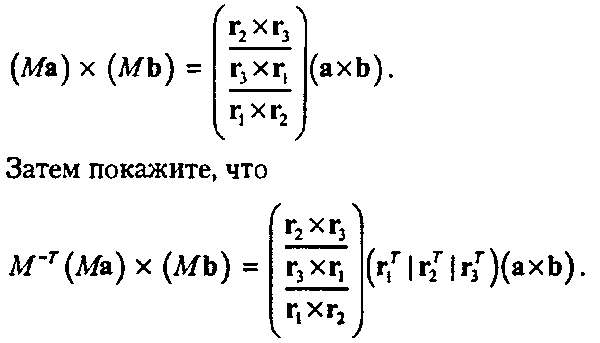
Наконец, покажите, что произведение первых двух матриц в правой части является диагональной матрицей, каждый диагональный элемент которой равен определителю матрицы М. {Подсказка: используйте свойства смешанного произведения а с х а - 0.)
Б2.3. Двойное векторное произведение Двойное векторное произведение (triple vector product - TVP) трех векторов a, b, с равно TVP - а х (b х с). Оно часто встречается при ручных вычислениях с применением векторных произведений. Двойное векторное произведение можно записать в виде разности двух масштабированных векторов:
На сайте http://www.cognac-whisky.ru коньяк элитный дорогой.
