1. Векторы а и а1 имеют одинаковую длину: |а| = 1а1!.
2. Линейность: (а + Ь)1 = а1 + Ъ1 и (Аа)1 = Аа1 для любого скаляра А.
3. Применение перпа дважды образует противоположный к а вектор: а11 = (а1)1 = -а.
Перп-скалярное произведение а1* Ь
1. Перп скалярного произведения а1- Ь = ар - аЬх.
2. а1- а = 0. (Перп а1 перпердикулярен вектору а.)
3. |ах|2 = |а|2. (Вектор а и его перп а1 имеют одинаковую длину.)
4. а1- Ь = -Ь1- а. (Перп-скалярное произведение антисимметрично.)
5. а1- Ь можно записать в форме определителя а а х у
К ъу
6. (а1-Ь)2 + (а-Ь)2 = |а|2|Ь|5.
7. Если а + Ь + с = 0, то а1- Ь = Ь1- с = с1- а.
8. а1- Ь > 0 тогда и только тогда, когда поворот от вектора а к вектору Ь производится против часовой стрелки (СС\У).
9. а1- Ь = 0, если вектор Ь параллелен или антипараллелен вектору а.
10. 1а1- Ь| равен площади параллелограмма, построенного на векторах а и Ь.
Б2. Некоторые свойства векторов и операции над ними Б2.2. Смешанное произведение Для трех пространственных векторов а, Ь, с существует очень полезная комбинация векторного и скалярного произведений. Чтобы определить эту величину для трех заданных векторов а, Ь и с, сформируем следующий скаляр:
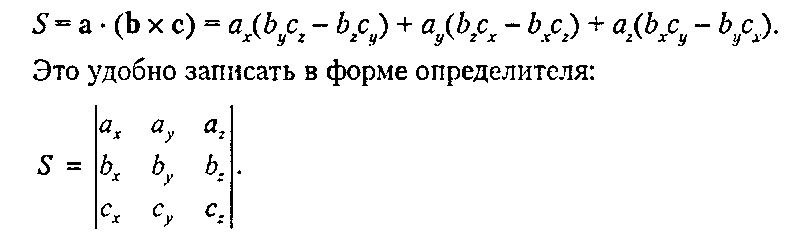
Перестановка строк в определителе приводит только к изменению его знака, поэтому двойная перестановка не приводит ни к каким изменениям. Следовательно, циклическая перестановка векторов не влияет на величину S, которая поэтому имеет три эквивалентных формы:
S = а (Ь х с) = b (с х а) = с (а х Ь).
Смешанное произведение (scalar triple product) имеет простую геометрическую интерпретацию (оно играет в трехмерном пространстве ту же роль, что и перп-скалярное произведение Ь1- с в двумерном): О Его модуль \S\ равен объему параллелепипеда, образованного векторами а, Ь, с, исходящими из одной точки.
О Знак смешанного произведения такой же, как у cos(0): последний положителен, если |0| < 90°, и отрицателен, если |0| > 90°. (Вопрос: изменится ли значение 5, если выразить векторы а, Ь, с в левосторонней системе координат?) Отметим, что если все три вектора лежат в одной и той же плоскости, то смешанное произведение будет равно нулю, так как объем соответствующего параллелепипеда в этом случае вырождается в нуль. Предположим, что ни один из векторов а, Ь, с не равен нулю. В этом случае смешанное произведение а (Ь х с) *= 0 тогда и только тогда, когда все три вектора компланарны (coplanar). (Вывод: три вектора являются компланарными, если Два из них параллельны.) Это свойство можно использовать при определении того, насколько плоским является полигон.
