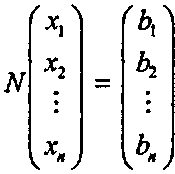
где заданы матрица N размерностью инапи вектор-столбец b, а требуется найти вектор х такой, чтобы все эти п уравнений удовлетворялись одновременно. Если N- невырожденная матрица (ее определитель не равен нулю), то решение может быть найдено как произведение х - ЛГЪ.
Тем не менее существует целый ряд методов решения такой системы уравнений, которые работают быстрее и более устойчивы к вычислениям, чем прямое вычисление матричного произведения ЛГ'Ь.
Отметим, что хотя в компьютерной графике превалирует применение векторов-столбцов, вышеприведенная система уравнений иногда записывается с использованием векторов-строк:
(xvx2.....хп)М~(Ьх,Ъ2,…,Ъп).
Нетрудно показать, что данная система уравнений совпадает с предыдущей, когда M - NT, а ее решение имеет вид х - ЪМ~1.
Ортогональные матрицы
Для некоторых преобразований, например для поворотов (см. главу 5), для соответствующих матриц найти обратную матрицу особенно просто. Матрица M называется ортогональной (orthogonal), если к ее обращению приводит ее простое транспонирование, то есть если Мт - М-1. Следовательно, ММТ= I. Если матрица M ортогональна, то из равенства ММГ=/следует, что каждая строка матрицы МпредставПриложение Б. Немного математики для компьютерной графики ляет собой вектор единичной длины и что строки взаимно ортогональны. То же верно и для столбцов матрицы М. (Почему?)
Например, если матрица М имеет размерность три на три, разобьем ее на три строки: М =
а с
Тогда каждая триада а, Ь, с имеет единичную длину иа-Ь = а- с = Ь- с = 0.
Б2. Некоторые свойства векторов и операции над ними Рассмотрим три операции над векторами: перп-скалярное произведение, смешанное произведение и двойное векторное произведение.
Б2.1. Перп вектора; перп-скалярное произведение Понятие перпа и перп-скалярного произведения применимо только к двумерным векторам.
Перп вектора Пусть имеется вектор а - (ах, ау). Тогда перпендикуляр к этому вектору, полученный поворотом исходного вектора на 90° против часовой стрелки, сокращенно именуемый «перп» («регр») и обозначаемый а1, определяется как а1 = (-я , ах). Перп имеет следующие свойства:
