О Если матрица В образована из матрицы М перестановкой двух строк (или двух столбцов) матрицы М, то \В\ - -\М\.
О Если матрица В образована из матрицы М умножением одной строки (или столбца) матрицы М на число к, то \В\ = к \М\.
О Если матрица В образована из матрицы М прибавлением произведения одной строки (или столбца) матрицы М на какое-либо число к другой ее строке, то \В\ - |М|.
Б1.5. Обращение матрицы
Матрица М размерностью п на п называется невырожденной (nonsingular), если ее определитель \М\ отличен от нуля. В этом случае матрица М имеет обратную (inverse) матрицу М'1, обладающую следующим свойством: мм-*-м-*м~1, где /- единичная матрица размерностью п на п. Кроме того, матрица, обратная к произведению квадратных матриц, имеет вид:
(АВу1 = В-1 А-К
Нетрудно выразить элементы обратной матрицы М-1 через алгебраические дополнения матрицы М. Пусть А - матрица, обратная к матрице М. Тогда ij-м элементом матрицы А будет число: а
Это означает, что мы находим алгебраическое дополнение элемента т~ и делим его на определитель всей матрицы. Обратите внимание на индексы: при вычислении элемента atj используется алгебраическое дополнение ту. Для нахождения обратной матрицы нужно проделать следующую последовательность операций.
1. Создайте промежуточную матрицу С из алгебраических дополнений c{j = Міу
2. Найдите определитель |М| как скалярное произведение любой строки матрицы С на соответствующую строку матрицы М.
3. Транспонируйте матрицу С и получите Ст.
4. Умножьте каждый элемент матрицы Ст на 1/|М|, чтобы получить М'К
Б1. Некоторые основные определения, относящиеся к матрицам и операциям над ними Пример
Обратите матрицу
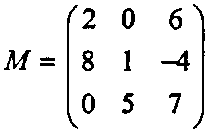
Решение Построим матрицу С из алгебраических дополнений матрицы М:
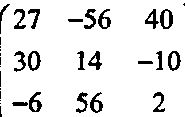
Далее найдем определитель |М| - (2,0,6) (27, -56,40) - 294. Теперь транспонируем матрицу С и умножим каждый ее элемент на 1/|М|, тогда получим:
f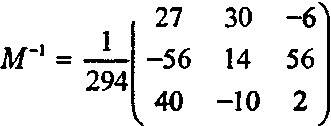
Проверьте получившийся результат посредством умножения ММ'1 и М~1М. В обоих случаях должна получиться единичная матрица /.
Обращение матриц часто используется при решении систем линейных уравнений (set of linear equations) вида
