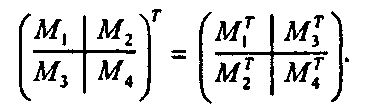
Две блочные матрицы можно также умножать посредством обычного матричного умножения их подматриц, если эти подматрицы являются согласованными:
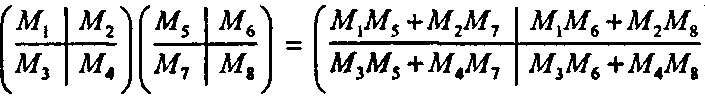
Б1.4. Определитель матрицы
С каждой квадратной матрицей М связано некоторое число, которое называется ее определителем (determinant) и обозначается |М| или detM. Определитель характеризует объем соответствующих геометрических брорм и содержит информацию о влиянии линейного преобразования на площади и объемы объектов.
Определитель матрицы два на два является просто разностью двух произведений:
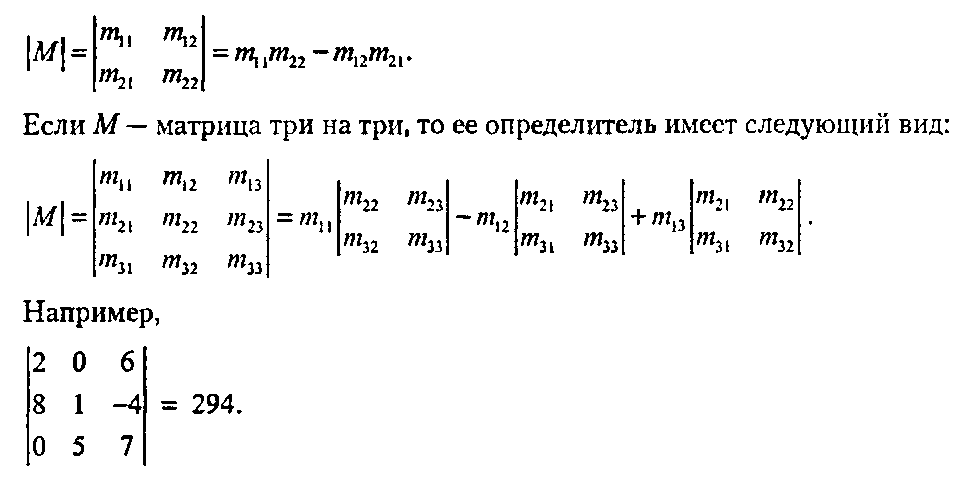
Отметим, что здесь определитель \М\ равен сумме следующих трех членов: тиМи + т12М12+ т13М13, в силу чего он имеет форму скалярного произведения: \М\ = (т,„ т12, т13) (М,,, Л/12, М13). Что означают элементы А/. ? М0 называется алгебраическим дополнением (сопг^ог) элемента матрицы М. Поскольку мы еще будем сталкиваться с алгебраическими дополнениями при обращении матриц, то дадим им формальное определение.
Определение. Каждому элементу квадратной матрицы М соответствует алгебраическое дополнение Мр равное произведению (-1)'+; на определитель матрицы, полученной при удалении из матрицы Мг-й строки и ./-го столбца.
Приложение Б. Немного математики для компьютерной графики Отметим, что при удалении строки или столбца множитель (-і)'*-* принимает значения 1 и -1. Это можно изобразить как наложенный на элементы матрицы шаблон из чисел 1 и -1, расположенных в шахматном порядке.
Существует общее правило нахождения определителя \М\ произвольной матрицы и на п: выберите любую строку матрицы М, найдите алгебраическое дополнение для каждого элемента этой строки и вычислите скалярное произведение этого ряда на я-кортеж, составленный из этих алгебраических дополнений. Можно также взять любой столбец матрицы М и произвести такую же операцию. (Действует ли это правило для матрицы два на два?)
Ниже приведены некоторые полезные свойства определителей: О |М|-|М|Г.
О Если два строки (или два столбца) матрицы М одинаковы, то |М| - 0. О Для двух квадратных матриц Ми В \МВ\ = \М\ \В\.
