Умножение вектора на матрицу
Частным случаем умножения матриц является случай, когда одна из матриц является вектором-строкой или вектором-столбцом. В графике часто встречается случай, когда матрица М умножается слева на вектор-столбец w, что обозначается Mw. Пусть, например
Приложение Б. Немного математики для компьютерной графики
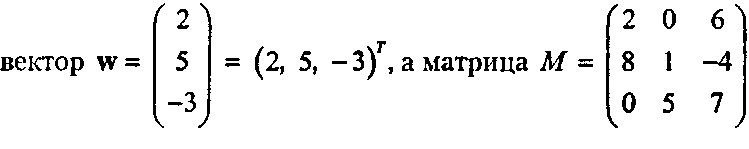
В данном случае вектор \у согласуется с матрицей М, следовательно, можно сформировать произведение
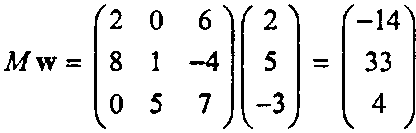
Согласно вышеприведенным правилам, каждый компонент матрицы М\у является скалярным произведением соответствующей строки матрицы М на вектор \у. Можно также умножить матрицу слева на вектор-строку V
Оранжевый рай клиника увлажнение кожи.
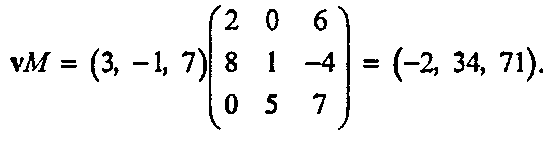
Снова скалярные и векторные произведения В ряде аналитических преобразований полезно записывать скалярное произведение а b двух кортежей (tuples) я-го порядка в форме произведения вектора на матрицу. Для этого рассмотрим вектор b как матрицу-строку и транспонируем ее в матрицу-столбец Ьг размерностью п на 1. Тогда а b - abr.
Из тех же самых соображений а b - Ьаг.
Аналогично векторное произведение двух триад а х b (см. раздел «Векторное произведение двух векторов» главы 4) можно записать в виде произведения
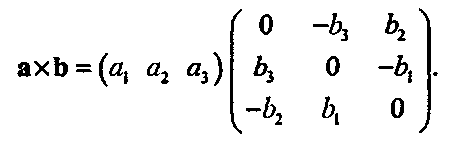
Векторное произведение также является матрицей (какой именно?), умноженной справа на вектор-столбец аг. Для еще одного вида произведения: внешнего, или тензорного произведения (outer or tensor product), существует полезная форма записи:
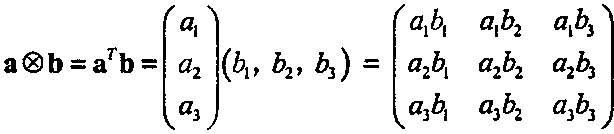
откуда следует, что Ь ® а - (а ® Ь)г. (Почему?) Легко доказывается также свойство а (Ь ® с) = (а Ь) с.
Б1.3. Разбиение матрицы на блоки Иногда полезно разбить матрицу на блоки из элементов и дать различным блокам свои имена. Например,
і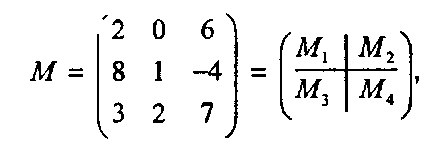
Б1. Некоторые основные определения, относящиеся к матрицам и операциям над ними
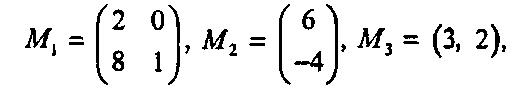
где входящие блоки равны соответственно: а М4 состоит из единственного элемента 7.
Это называется разбиением (partition) матрицы М на четыре указанных блока. Отметим, что когда один блок находится над другим, то эти блоки должны иметь одинаковое число столбцов. Когда же два блока располагаются рядом, то они должны иметь одинаковое число строк. Две блочные (partitioned) матрицы, разбиение которых было произведено одинаково (соответствующие блоки имеют одинаковую размерность), можно складывать поблочно. Для транспонирования блочных матриц следует транспонировать каждый блок по отдельности и затем транспонировать расположение блоков. Таким образом,
