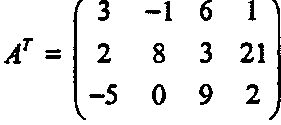
Результатом транспонирования вектора-строки является вектор-столбец. Например,
1 В некоторых источниках размерность называют структурой матрицы. - Примеч. пер.
Б1. Некоторые основные определения, относящиеся к матрицам и операциям над ними
Матрица называется симметричной (symmetric), если она не изменяется при транспонировании. Симметричными могут быть только квадратные матрицы. Таким образом, матрица М размерностью п х п является симметричной, если = ти.; для всех z и j от 1 до п.
Б1.2. Умножение двух матриц
Преобразования, впервые рассматриваемые в главе 5, включают в себя умножение вектора на матрицу и умножение двух матриц друг на друга. Первое понятие является частным случаем второго.
Произведение (product) АВ двух матриц Л и Б определено только в том случае, если эти две матрицы являются согласованными (conform). Это означает, что число столбцов первой матрицы А равно числу строк второй матрицы В. Таким образом, если матрица Л имеет размерность 3 х 5, а матрица В - 5 х 2, то произведение АВ определено, а произведение ВА - нет. Каждый элемент произведения С матриц А и В С - АВ является скалярным произведением некоторой строки матрицы А на некоторый столбец матрицы В. А именно, ij-й элемент е.. этого произведения является скалярным произведением 2-Й строки матрицы А на j-й столбец матрицы В. Тогда произведение матрицы размерностью пхтна матрицу тхг будет матрицей пхг. Пример:
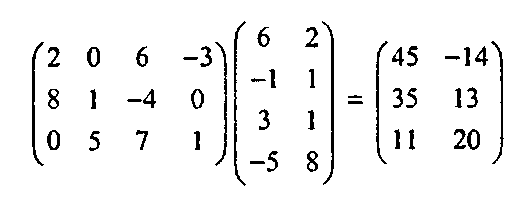
Здесь, например, элемент с12 = -14, поскольку (2, 0, б, -3)(2, 1, 1, 8) = -14. Подпрограмма умножения квадратных матриц приведена в приложении В; ее легко расширить для нахождения произведения двух любых согласованных матриц.
Перечислим некоторые полезные свойства умножения матриц. Пусть матрицы Л, В, С согласуются должным образом. Тогда
(АВ)С = А(ВС), А(В + С)-=ЛВ + АС, (А + В)С = АС + ВС, (АВ)Т = ВТЛТ, A (sB) = sAB, где s - число.
При формировании произведения двух матриц А и В имеет значение порядок следования этих матриц. О выражении АВ мы говорим: «А умножается слева (premultiplies) на В» или «Б умножается справа (postmultiplied) на Л». Если обе матрицы Л и В - квадратные матрицы одной и той же размерности, то оба произведения - АВ и ВА - определены, однако эти два произведения могут содержать различные элементы. Если для двух матриц АВ = ВА, то эти две матрицы называются коммутативными (commute). (Всегда ли коммутативны две симметричные матрицы?)
