Отдельные элементы матрицы обычно обозначаются строчными буквами с различными нижними индексами: г/'-й элемент матрицы В обозначается Ь^. Это элемент f-й строки и ./-го столбца. Например, для матрицы А из уравнения (А2.1) элемент а32 = 3.
Приложение Б. Немного математики для компьютерной графики Матрица называется квадратной (square), если число ее строк и столбцов одинаково. В графике мы часто имеем дело с матрицами размерностью два на два, три на три и четыре на четыре. Часто используются следующие два типа квадратных матриц: нулевая матрица (zero matrix) и единичная матрица (identity matrix). Все элементы нулевой матрицы равны нулю. У единичной матрицы равны нулю все элементы, за исключением элементов главной диагонали (main diagonal) а. (у которых г = j), которые равны единице. Следовательно, единичная матрица три на три имеет вид: Б1.1. Действия с матрицами Числовая матрица В может быть масштабирована (scaled) числом s (умножена на число 5). При этом каждый элемент матрицы В умножается на s. Полученная матрица обозначается sB. К примеру, для матрицы А из уравнения (А2.1) получим:
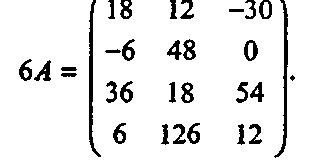
Две матрицы С и Д имеющие одинаковое число строк и столбцов, называются матрицами одинаковой размерности (shape)1, и их можно складывать. Элемент ij этой суммы Е - С + D является просто суммой соответствующих элементов: е.. - с. + djy Например,
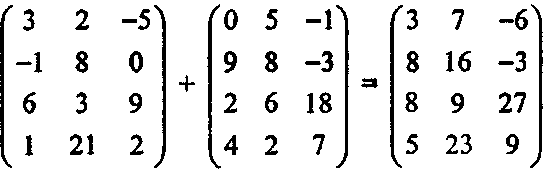
Поскольку матрицы можно масштабировать и складывать, имеет смысл определить линейные комбинации (linear combinations) матриц (одинаковой размерности), например, 2А - 45. Из определений сложения и масштабирования непосредственно следуют свойства коммутативности, ассоциативности и дистрибутивности для трех матриц А, В, С одинаковой размерности: А + В-В + А; А + (В + С)-(А + В) + С;
(f+g)(A + B)-fA+fB + gA + gB.Результат транспонирования (transpose) матрицы М, обозначаемый Мт, образуется посредством перестановки (взаимной замены) строк и столбцов матрицы М: ij-й элемент матрицы Мт равен ji-uy элементу матрицы М. Например, транспонирование матрицы А из уравнения (А2.1) дает:
