real = (tempreal * tempreal) - (imag * imag) + Creal; imag = 2.0 * tempreal * imag + Cimag: r2 = (real * real) + (imag * imag):
}
// Цвет зависит от количества итераций
vec3 color;
if (r2 < 4.0)
color = InnerColor; el se
color = mix(OuterColorl, 0uterColor2, fract(iter * 0.05)): color *= Lightlntensity; gl_FragColor = vec4 (color. 1.0);
}
Очевидно, что этот шейдер можно совершенствовать. Сначала можно усовершенствовать алгоритм выбора цвета, например, используя одномерную текстуру для хранения значений цвета. Количество итераций в этом случае может служить индексом в текстурной таблице.
После выбора приятного набора цветов можно рассмотреть несколько популярных частей множества Мандельброта. Различные книги и веб-сайты публикуют ко ординаты интересных частей множества, и эти шейдеры исполнены таким образом, чтобы можно было самому ввести координаты и сразу увидеть результаты (рис. 15.8).

Рис. 15.8. Результаты работы шейдера Мандельброта
15.3.4. Множества Джулии
Множества Джулии немного похожи на множество Мандельброта. Каждая точка в множестве Мандельброта может использоваться для создания множества Джулии, и эти новые множества не менее интересны. Единственное их отличие в том, что константа с в уравнении Z2 + с устанавливается в значение какой-нибудь точки, входящей в множество Мандельброта (кроме той, которую рисуют в данный момент). Чтобы изменить фрагментный шейдер соответствующим образом, нужно поменять две строки кода, инициализирующие значение с:
float Creal = -1.36: // Теперь мы увидим интересное множество
float Cimag = 0.11; На рис. 15.9 показано несколько примеров множеств Джулии, которые можно создавать с помощью этого шейдера. Для этого можно параметризовать значения Сгеа 1 и Cimag, передавая их через uniform-переменные.
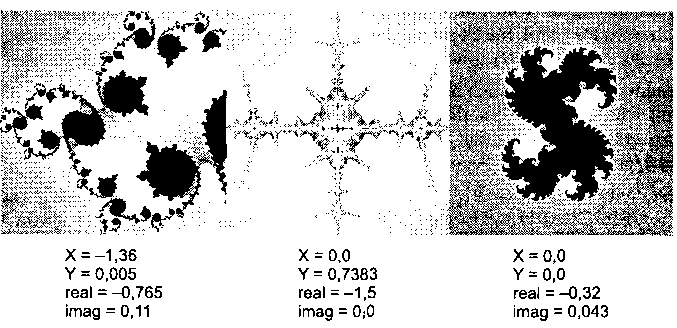
Рис. 15.9. Множества Джулии, нарисованные шейдером Мандельброта
15.4. Итоги
Далеко не во всех интерактивных графических программах нужен реализм. Используя современные возможности графического аппаратного обеспечения, легко можно создавать любые нужные эффекты. С помощью высокоуровневого процедурного языка, такого как язык шейдеров OpenGL, художники и создатели графических программ могут программировать алгоритмы для рисования в художественных стилях, имитируя, например, перо, гравюру, живопись. В этой главе был представлен процедурный шейдер штриховки, который иллюстрирует процесс создания таких шейдеров. Различные виды технических иллюстраций можно создавать с помощью шейдера Гуча, описанного в этой главе. Можно также создавать шейдеры для визуализации математических функций, например шейдеры Мандельброта и Джулии.
История искусства давно доказала, что существует бесконечное множество художественных стилей. С помощью языка шейдеров OpenGL можно создавать шейдеры, имитирующие некоторые из этих стилей и, возможно, создающие новые стили.
15.5. Ссылки
Нефотореалистичному рендерингу посвящены книги [10 и 16].
Алгоритм Гуча определен и описан в докладе [8]. Доклад основан на принципах, описанных Эдвардом Тафте в 1997 г. Небольшое обсуждение NPR приводится в книге ШКлассическое описание фракталов и множества Мандельброта приведено в книге [12]. В 1986 г. Хайнц-Отто Питжен и Петер Рихтер написали книгу [14].
