Если рассматривать каждую сторону многоугольника как вектор, то в проверке на вогнутость может использоваться векторное произведение двух соседних сторон. Для выпуклого многоугольника все такие векторные произведения будут одного знака (положительные или отрицательные). Следовательно, если одни векторные произведения будут положительными, а другие - отрицательными, то данный многоугольник - вогнутый. На рис. 3.43 показана реализация метода векторных произведений сторон многоугольника для распознавания вогнутых многоугольников.
Еще один способ распознавания вогнутых многоугольников - изучить положения вершин многоугольника относительно продолжения любой из его сторон. Если некоторые вершины находятся по одну сторону от такого продолжения, а некоторые - по другую, то такой многоугольник относится к вогнутым.
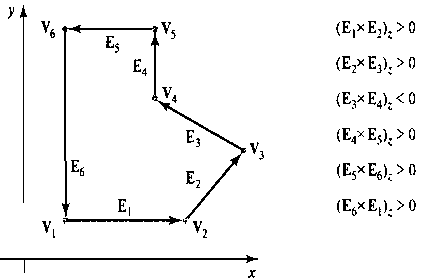
Рис. 3.43. Для распознавания вогнутых многоугольников последовательно вычисляются векторные произведения пар векторов сторон
ДЕЛЕНИЕ ВОГНУТЫХ МНОГОУГОЛЬНИКОВ
Вогнутый многоугольник можно разделить на набор выпуклых с помощью векторов сторон и их векторных произведений или, используя положения вершин относительно линии продолжения одной из сторон, определить, какие вершины находятся по одну сторону от этой линии, а какие - по другую. Для реализации следующих алгоритмов допустим, что все многоугольники расположены в плоскости ху. Разумеется, исходный многоугольник, описанный во внешних координатах, может и не лежать в плоскости ху, но его всегда можно переместить в эту плоскость, воспользовавшись методами преобразований, описанными в главе 5.
Далее нужно найти векторные произведения соседних векторов сторон по порядку по всему периметру многоугольника. Если компонент г одних векторных произведений будет положительным, а других - отрицательным, то многоугольник вогнутый. В противном случае многоугольник выпуклый. Здесь предполагается, что среди вершин нет трех последовательных коллинеарных точек, поскольку в таком случае векторное произведение двух векторов сторон, содержащих эти вершины, будет равно нулю. Если все вершины коллинеарные, то многоугольник вырожден (представляет собой прямую линию). Векторный метод можно применять, обрабатывая стороны последовательно против часовой стрелки. Если у какого-то векторного произведения появится отрицательный компонент г (как на рис. 3.43), то многоугольник - вогнутый, и его можно разделить, продолжив первый вектор стороны из той пары векторов, произведение которых рассматривается. Описанный метод разделения вогнутого многоугольника иллюстрируется в следующем примере.
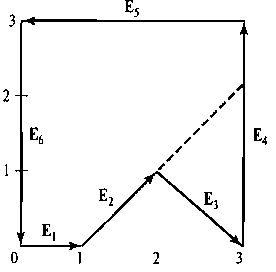
Рис. 3.44. Разделение вогнутого многоугольника с помощью векторного метода
РАЗДЕЛЕНИЕ ВЫПУКЛОГО МНОГОУГОЛЬНИКА НА НАБОР ТРЕУГОЛЬНИКОВ
Если дан список вершин выпуклого многоугольника, его можно преобразовать в набор треугольников. Для этого сначала определяется любая последовательность из трех идущих подряд вершин, которые образуют новый многоугольник (треугольник). После этого из исходного списка вершин удаляется средняя вершина треугольника. Затем та же процедура выполняется с измененным списком вершин, и вырезается еще один треугольник. Формирование треугольников продолжается до тех пор, пока исходный список вершин многоугольника не уменьшится до трех, которые и определят координаты вершин последнего треугольника этого набора. С помощью этого метода вогнутый многоугольник также можно разделять на набор треугольников, продолжая процесс до тех пор, пока три выбранные вершины на каждом этапе будут образовывать внутренний угол, не превышающий 180° (“выпуклый” угол).
