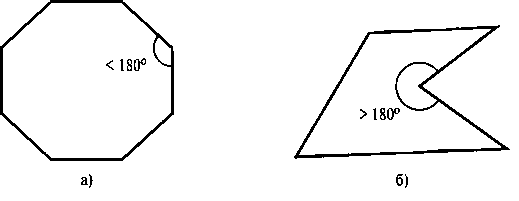
Рис. 3.42. Многоугольники: а) выпуклый; б) вогнутый ной поверхности набором многоугольных участков. Один из способов исправления этой ситуации - просто разделить заданную сетку многоугольников на треугольники. Однако в некоторых случаях могут существовать причины, по которым необходимо сохранить изначальный вид ячеек сетки, поэтому были придуманы методы аппроксимации неплоских многоугольных фигур плоскими объектами. Расчет таких плоских аппроксимаций будет обсуждаться в подразделе, касающемся уравнений плоскости.
КЛАССИФИКАЦИЯ МНОГОУГОЛЬНИКОВ
Внутренним углом многоугольника называется угол внутри границы многоугольника, образованный двумя соседними сторонами. Если все внутренние углы многоугольника меньше или равны 180°, то многоугольник выпуклый. Существует эквивалентное определение выпуклого многоугольника - весь многоугольник должен лежать по одну сторону от бесконечной прямой, являющейся продолжением любой из его сторон. К тому же, если выбрать любые две точки внутри выпуклого многоугольника, то прямолинейный отрезок, соединяющий эти точки, также будет полностью находиться внутри многоугольника. Многоугольник, который не является выпуклым, называется вогнутым. На рис. 3.42 приведены примеры выпуклого и вогнутого многоугольников.
Термином вырожденный многоугольник часто описывают набор вершин, которые являются коллинеарными или координаты которых повторяются. Коллинеарные вершины дают прямолинейный отрезок. Вершины с повторяющимися координатами могут дать многоугольную фигуру с лишними линиями, перекрывающимися сторонами или сторонами, длина которых равна 0. Иногда термин вырожденный многоугольник еще применяется к списку вершин, который состоит из менее, чем трех точек.
Устойчивые графические пакеты могут не воспринимать вырожденные или неплоские наборы вершин. Однако их распознавание требует дополнительной обработки, поэтому в графических системах выбор ограничивающих условий, как правило, оставляется на усмотрение программиста.
Вогнутые многоугольники также создают дополнительные проблемы. Реализация алгоритмов закрашивания и других графических процедур для вогнутых многоугольников намного сложнее, поэтому, как правило, перед обработкой эффективнее разделить вогнутый многоугольник на набор выпуклых. Как и другие алгоритмы предварительной обработки многоугольников, функции разделения вогнутого многоугольника часто не входят в графическую библиотеку. Для некоторых пакетов, в том числе и OpenGL, необходимо, чтобы все закрашиваемые многоугольники были выпуклыми. Кроме того, в некоторых системах допускается только закрашивание треугольных областей, что значительно упрощает многие алгоритмы создания изображений.
РАСПОЗНАВАНИЕ ВОГНУТЫХ МНОГОУГОЛЬНИКОВ
У вогнутого многоугольника по крайней мере один внутренний угол больше, чем 180°. Кроме того, продолжения некоторых сторон вогнутого многоугольника будут пересекать другие ребра, а некоторые пары внутренних точек дадут отрезки, пересекающие границы многоугольника. Следовательно, любой из этих признаков вогнутого многоугольника можно положить в основу алгоритма распознавания вогнутых многоугольников.
