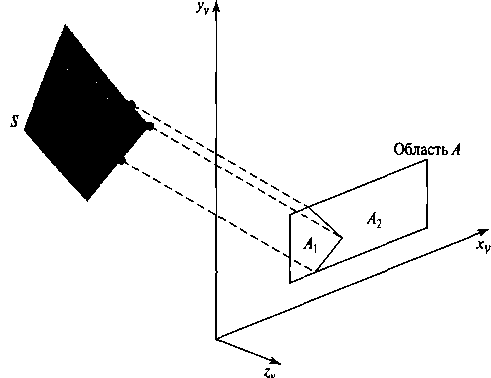
Рис. 9.23. Область А делится на А\ и А2 с помощью границы поверхности 5 на плоскости наблюдения Возможна небольшая модификация базового процесса деления - вместо того, чтобы делить области пополам, их можно делить вдоль границ поверхностей. Если поверхности были отсортированы согласно минимальной глубине, для деления данной области используется поверхность с наименьшим значением глубины. Сказанное иллюстрируется на рис. 9.23. Проекция границы поверхности 5 делит исходную область на подобласти А1 и А2. После этого поверхность 5 является окружающей поверхностью для А\, и, чтобы определить, требуется ли дальнейшее деление, можно проверять условия видимости 2 и 3. Вообще, чтобы при описанном подходе разделить области и проанализировать отношения поверхностей к границам деления, требуется меньше делений, но больше обработки.
МЕТОДЫ ОКТОДЕРЕВЬЕВ
Когда в наблюдаемом объеме используется представление в форме восьмеричного дерева (октодерево, octree), выявление видимых поверхностей выполняется через поиск в пространстве узлов октодерева в порядке от переднего к заднему плану. На рис. 9.24 передний план сцены занимают октанты 0,1,2 и 3. Поверхности перед этими октантами видимы для наблюдателя. Любые поверхности, расположенные позади передних октантов или в задних октантах (4, 5, 6 и 7), могут быть скрыты передними поверхностями.
Узлы октодерева на рис. 9.24 можно обработать в порядке 0, 1, 2, 3, 4, 5, 6, 7. Эго соответствует прохождению дерева вглубь, причем узлы четырех передних под-окгантов октанта 0 видимы перед узлами четырех задних подоктантов. При каждом делении октанта прохождение октодерева выполняется в таком порядке.
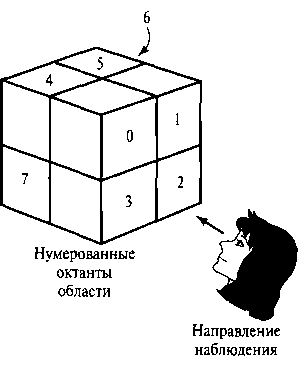
Рис. 9.24. При указанном направлении наблюдения объекты в октантах 0, 1, 2 и 3 затеняют объекты в задних октантах (4, 5, 6, 7)
Когда при проходе восьмеричного дерева встречается код цвета, данный цвет записывается в квадродереве, только если для этой же области ранее не было записано ни одного значения. При таком подходе записываются только цвета передних граней. Узлы, имеющие значение “пусто” (“void”), игнорируются. Любой полностью затеняемый узел исключается из дальнейшей обработки, так что его поддеревья недоступны. На рис. 9.25 изображены октанты области пространства и соответствующие квадранты на плоскости наблюдения. Вклады в квадрант 0 дают октанты 0 и 4. Коды цвета в квадранте 1 определяют поверхности в октантах 1 и 5, а коды в остальных двух квадрантах генерируются по значениям в парах октантов, соотнесенных с этими квадрантами.
Эффективно проверить видимость по октодереву позволяет рекурсивная обработка узлов октодерева и создание квадродерева для видимых поверхностей. В большинстве случаев нужно рассмотреть и передний, и задний октант, чтобы определить правильный код цвета квадранта. Однако, если передний октант однородно закрашен некоторым цветом, задний октант не обрабатывается. Для неоднородных областей вызывается рекурсивная процедура, возвращающая в качестве новых аргументов потомки неоднородного октанта и свежесозданные узлы квадродерева. Если передний октант пуст, необходимо обработать только потомки заднего октанта. В противном случае делается два рекурсивных вызова, один для заднего октанта, один для переднего.
