Существует четыре возможные связи, которые поверхность может иметь с областью разделенной плоскости наблюдения. Данные относительные положения поверхности можно описать, используя следующие классификации (рис. 9.21).
Рис. 9.20. Деление квадратной области на каждом шаге на квадраты равного размера

Рис. 9.21. Возможные связи между многоугольными поверхностями и прямоугольной областью плоскости наблюдения Окружающая поверхность: поверхность, полностью замыкающая область.
Накладывающаяся поверхность: поверхность, расположенная частично внутри и снаружи области.
Внутренняя поверхность: поверхность, расположенная целиком внутри области.
Внешняя поверхность: поверхность, расположенная полностью вне области.
Проверки на определение видимости поверхности в пределах прямоугольной области можно сформулировать в терминах четырех классификаций поверхности, проиллюстрированных на рис. 9.21. Дальнейшее деление указанной области не требуется, если выполняется одно из приведенных ниже условий.
Условие 1: область не принадлежит к внутренним, накладывающимся или окружающим поверхностям (все поверхности находятся вне области).
Условие 2: область имеет только одну внутреннюю, накладывающуюся или окружающую поверхность.
Условие 3: область имеет одну окружающую поверхность, затеняющую все остальные поверхности в пределах границ области.

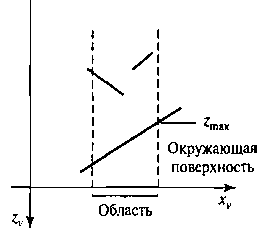
Рис. 9.22. В заданной области окружающая поверхность с максимальной глубиной 2тах затеняет все поверхности, минимальная глубина которых превышает гтах
Первый шаг анализа - сравнение координатных границ всех поверхностей в пределах границ области. Это определит внутренние и окружающие поверхности, но выявление накладывающихся и внешних поверхностей обычно требует проверок на пересечение. Если первый граничный прямоугольник пересекает область, то, чтобы определить, является поверхность окружающей, накладывающейся или внешней, используются дополнительные проверки. Как только выявлена внутренняя, накладывающаяся или окружающая поверхность, в буфер кадров записываются ее коды цвета.
Чтобы проверить условие 3, можно, например, рассортировать поверхности согласно минимальной глубине от плоскости наблюдения. Затем для каждой окружающей поверхности вычисляется максимальная глубина в пределах рассматриваемой области. Если максимальная глубина (отсчитывается от плоскости наблюдения) одной из таких окружающих поверхностей меньше, чем минимальная глубина всех остальных поверхностей данной области, условие 3 удовлетворяется. Данная ситуация иллюстрируется на рис. 9.22.
Другой метод проверки условия 3, не требующий сортировки по глубине, - это использовать уравнения плоскости для расчета значений глубин в четырех вершинах области для всех окружающих, накладывающихся и внутренних поверхностей. Если все четыре глубины для одной поверхности меньше рассчитанных глубин для всех остальных поверхностей, условие 3 удовлетворено. Далее область можно отобразить с цветами окружающей поверхности.
В некоторых ситуациях предыдущие два метода проверки могут не выявить окружающую поверхность, затеняющую все остальные. Чтобы правильно определить поверхность, охватывающую область, можно продолжить проверку, но проще эту область разделить. Поверхность, классифицированная как внешняя или окружающая для данной области, будет оставаться в этой категории при всех делениях области. Более того, можно ожидать, что при продолжении процесса деления исчезнут некоторые внутренние и накладывающиеся поверхности, так что анализировать области будет проще. Когда деление доходит до размера пикселя, в каждой точке просто рассчитывается глубина значимой для нее поверхности, и пикселю присваивается цвет ближайшей поверхности.
