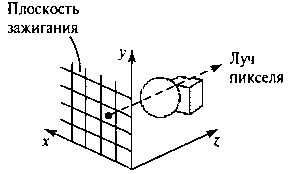
Рис. 8.60. Реализация операций конструктивной стереометрии с использованием схемы расчета луча
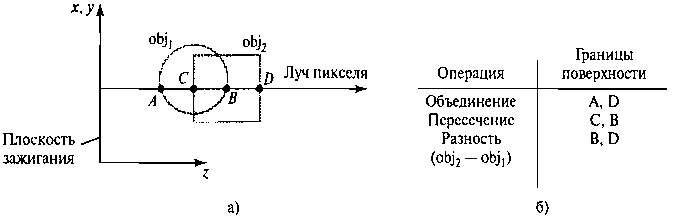
Рис. 8.61. Определение границ поверхности вдоль луча пикселя Методы расчета луча широко используются для реализации операций конструктивной стереометрии, когда объекты описываются контурными представлениями. Чтобы применить расчет луча, определяются объекты, которые пересекаются набором параллельных прямых, проходящих через плоскость ху по направлению оси г. Данная плоскость называется плоскостью зажигания, а каждый луч начинается в положении пикселя, как показано на рис. 8.60. Затем точки пересечения каждого луча с поверхностями вычисляются и сортируются согласно расстоянию от плоскости зажигания. Далее с помощью заданных операций над множествами определяются границы поверхности сложного объекта. Пример определения границ поверхностей с помощью расчета луча для СБО-объекта приведен на рис. 8.61, где показаны поперечные сечения в плоскости у г двух объектов (блока и сферы) и траектория луча пикселя, перпендикулярного плоскости зажигания. После операции логического сложения новый объем является суммарной внутренней частью, занятой двумя объектами. После операции пересечения новый объем - это внутренняя область, общая для обоих объектов. Наконец, операция вычитания отнимает одну внутреннюю часть объекта от другой в области пересечения двух объектов.
Каждый СБв-примитив обычно определяется в локальных (модельных) координатах. Соответствующие точки во внешней системе координат определяются с помощью матрицы модельного преобразования, используемой для наложения данного объекта на другой. Матрицы, обратные к модельным матрицам объектов, можно использовать для преобразования лучей пикселей в модельные координаты, где расчет точек пересечения с поверхностью выполняется для отдельных примитивов. Затем точки пересечения с поверхностями двух совмещенных объектов сортируются согласно расстоянию от начала луча пикселя и используются для определения границ составного объекта согласно заданной операции над множествами. Данная процедура повторяется для каждой пары объектов, которые нужно объединить в СБв-дерево искомого объекта.
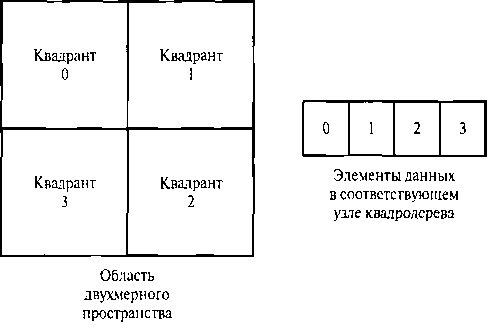
Рис. 8.63. Квадратная область на плоскости ху, разделенная на нумерованные квадранты, и соответствующий узел квадродерева с четырьмя элементами данных
Подобные выражения можно получить для других физических свойств (центр масс и момент инерции). Приближенный расчет физических свойств можно улучшить, введя дополнительные лучи для подпикселей плоскости зажигания.
Если формы объектов представлены октодеревьями, операции над множествами в процедурах CSG можно реализовать, сканируя древовидную структуру, описывающую содержимое пространственных октантов. В данной процедуре, описанной в следующем разделе, в октантах и подоктантах единичного куба выполняется поиск областей, занятых двумя совмещаемыми объектами.
ОКТОДЕРЕВЬЯ
В некоторых графических системах для представления объемных объектов используются иерархические древовидные структуры, называемые октодеревьями (octrees). Представления в форме октодеревьев широко используются в сфере построения медицинских изображений и других приложениях, требующих отображения поперечных сечений объектов. Древовидная структура организована так, что каждый узел соответствует области трехмерного пространства. Это представление объемных тел использует пространственную когерентность, чтобы снизить требования к памяти для хранения трехмерных объектов. Кроме того это представление удобно для хранения информации о внутренних областях объектов.
