Когда линия пересекает границу отсечения, но не входит во внутреннюю часть объема наблюдения, обработка отрезка продолжается, как и в соответствующем двухмерном алгоритме. Участок линии, расположенный вне этой границы отсечения, удаляется, и для части отрезка, находящейся внутри этой границы, обновляется информация по кодам области и значения параметра и. Затем проверяются оставшиеся участки линии с другими плоскостями отсечения на предмет возможного отклонения отрезка или поиска точки пересечения.
Отрезки на трехмерных сценах обычно не появляются обособленно. Чаще всего они служат компонентами описания объемных объектов на сцене, и обработка линий является необходимой частью процедур отсечения поверхностей.
ТРЕХМЕРНОЕ ОТСЕЧЕНИЕ МНОГОУГОЛЬНИКОВ
В графических пакетах обычно обрабатываются только сцены, содержащие “графические объекты”. Так называются объекты, границы которых описываются линейными
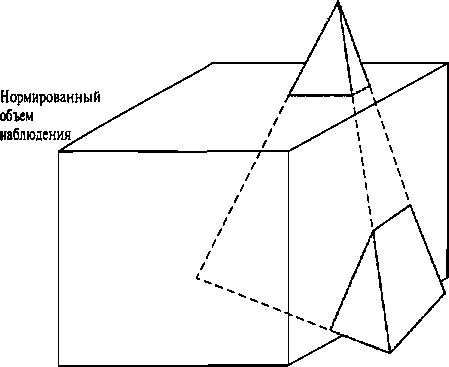
Рис. 7.59. Трехмерное отсечение объектов. Участки поверхности, лежащие внутри плоскостей отсечения объема наблюдения, удаляются из описания объекта, при этом, возможно, потребуется построить новые грани уравнениям, так что каждый объект составлен из наборов многоугольных поверхностей. Следовательно, чтобы выполнить отсечение объектов на трехмерной сцене, процедуры отсечения применяются к многоугольным поверхностям. На рис. 7.59, например, подсвечены участки поверхности пирамиды, которые будут отрезаны, а пунктиром показаны участки многоугольных поверхностей, принадлежащие объему наблюдения.
Вначале многогранник можно проверить на тривиальное принятие или отклонение, используя его координатные границы, ограничивающую сферу или какую-то другую меру его координатных границ. Если координатные границы объекта принадлежат всем границам отсечения, объект записывается целиком. Если все координатные границы лежат за любой из границ отсечения, весь объект удаляется.
Когда объект нельзя принять или отбросить целиком, можно обработать списки вершин набора многоугольников, определяющего поверхности объекта. Применяя методы, подобные описанным для двухмерного отсечения многоугольников, можно отсекать стороны, формируя новые списки вершин поверхностей объекта. Возможно, также придется создать несколько новых списков вершин для дополнительных поверхностей, возникших в результате операций отсечения. Кроме того, таблицы многоугольников обновляются, чтобы включить в них новые многоугольные поверхности и проверить информацию о связности и общих сторонах поверхностей.
Чтобы упростить отсечение произвольных многогранников, многоугольные поверхности часто делятся на треугольные участки и описываются треугольными фрагментами. В таком случае для отсечения можно использовать подход Сазерленда-Ходгмана, рассмотренный в разделе 3.15. Каждая полоса из треугольников обрабатывается последовательно шестью плоскостями отсечения, и на выходе получается конечный список вершин полосы.
Для вогнутых многоугольников можно применить методы расщепления (раздел 3.15) и получить, например, набор треугольников, а затем выполнить их отсечение. Как вариант, обработку вогнутых трехмерных многоугольников можно проводить с помощью алгоритма Уэйлера-Азертона, описанного в разделе 6.8.
