}

Рис. 7.55. Выходное изображение, сгенерированное программой трехмерного наблюдения
ТРЕХМЕРНЫЕ АЛГОРИТМЫ ОТСЕЧЕНИЯ
В главе 6 обсуждались преимущества использования нормированных границ отсекающего окна в двухмерных алгоритмах отсечения. Подобным образом трехмерные алгоритмы отсечения можно применить к нормированным границам объема наблюдения. Это позволяет крайне эффективно реализовать конвейер проектирования и процедуры отсечения. Все аппаратно-независимые преобразования (геометрические и проектирования) сворачиваются и применяются до выполнения процедур отсечения. В трехмерном случае каждая граница отсечения нормированного объема наблюдения представляет собой плоскость, параллельную одной из декартовых плоскостей, вне зависимости от типа проекции и исходной формы объема наблюдения.
Если однородный параметр /г равен 1, однородные координаты аналогичны декартовым координатам проекции. Такая ситуация часто возникает при параллельном проектировании. Однако перспективная проекция дает однородный параметр, который является функцией координаты г любой точки пространства. Однородный параметр перспективной проекции может даже быть отрицательным. Так бывает, когда точки располагаются за центром проекции. Кроме того, представления поверхностей объектов рациональными сплайнами часто формулируются в однородных координатах, где однородный параметр может быть положительным или отрицательным. Следовательно, если отсечение выполняется в координатах проекции после деления на однородный параметр к, некоторая координатная информация может теряться, и объекты не будут отсекаться корректно.
Чтобы эффективно обрабатывать все возможные проекционные преобразования и представления объектов, следует применить процедуры отсечения к представлению точек пространства в однородных координатах. Кроме того, поскольку все объемы наблюдения можно преобразовать в нормированный куб, на аппаратном уровне можно реализовать единственную процедуру отсечения, обрабатывающую объекты в однородных координатах нормированными плоскостями отсечения.
ТРЕХМЕРНЫЕ КОДЫ ОБЛАСТЕЙ
Расширим концепцию кода области (раздел 6.7) на три измерения, просто введя пару дополнительных разрядов для учета ближней и дальней плоскостей отсечения. Таким образом, теперь будет использоваться шестиразрядный код области, как показано на рис. 7.56. Разряды в этом примере нумеруются справа налево и соответствуют левой, правой, нижней, верхней, ближней и дальней плоскостям отсечения (в таком порядке).
ТРЕХМЕРНОЕ ОТСЕЧЕНИЕ ТОЧЕК И ЛИНИЙ
Для обычных точек и отрезков, определенных на сцене, которая не лежит позади центра проекции, все однородные параметры положительны, и коды областей можно установить, используя условия (7.47). Затем, определив для каждой точки на сцене код области, можно легко найти положения точек, входящих или не входящих в объем наблюдения. Например, код области 101000 сообщает, что точка находится над объемом наблюдения и позади него, а код области 000000 указывает на внутреннюю
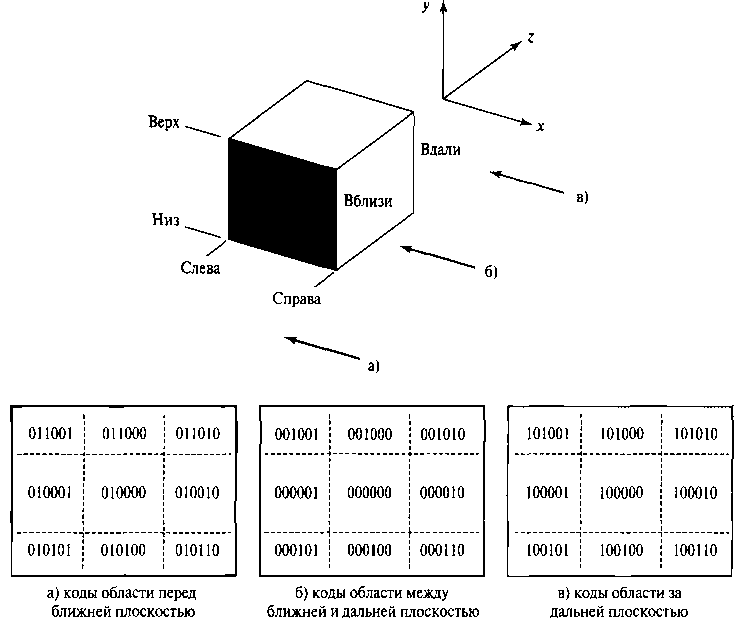
Рис. 7.57. Значения трехмерного шестиразрядного кода области, идентифицирующие пространственные положения относительно границ объема наблюдения
