ОБРАБОТКА МНОГОУГОЛЬНИКА С ИСПОЛЬЗОВАНИЕМ ОТСЕКАЮЩИХ ОКОН С НЕЛИНЕЙНЫМИ ГРАНИЦАМИ

Один метод обработки с помощью отсекающего окна с криволинейными границами заключается в аппроксимации границ прямыми отрезками и использовании одного из алгоритмов отсечения с помощью многоугольного окна. В качестве альтернативы можно использовать те же общие процедуры, что обсуждались для отрезков. Во-первых, можно сравнить координатные границы закрашенной области с координатными границами отсекающего окна. В зависимости от формы отсекающего окна также возможны другие проверки областей, основанные на соображениях симметрии. Для закрашенных областей, которые нельзя однозначно отнести к внутренним или внешним, в конечном итоге потребуется вычислить точки пересечения закрашенной области с окном.

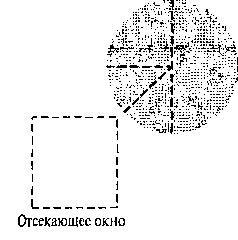
Рис. 6.31. Круговая закрашенная область, демонстрирующая квадрант и октант, находящиеся вне границ отсекающего окна

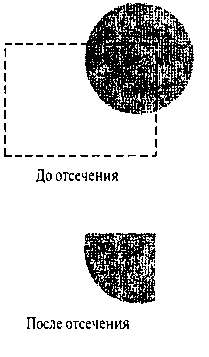
Рис. 6.32. Отсечение круговой закрашенной области

ОТСЕЧЕНИЕ КРИВЫХ

Области с криволинейными границами можно подвергать отсечению, используя методы, подобные рассмотренным в предыдущих разделах. Если объекты аппроксимируются прямыми отрезками, используются методы отсечения многоугольников. В противном случае процедуры отсечения включают нелинейные уравнения, а следовательно, требуют больше обработки для объектов с нелинейными границами.

Итак, вначале можно сравнить координатные границы объекта с границами отсечения, определив, можно ли тривиально принять или отклонить объект целиком. Если нет, проверяется симметрия объекта, которую, возможно, удастся использовать в первоначальных проверках принятия-отклонения. Например, окружности имеют симметричные квадранты и октанты, так что можно проверять координатные границы этих отдельных секторов окружности. Всю круговую область, показанную на рис. 6.31, нельзя отклонить полностью, просто проверив ее общие координатные границы. Однако половина окружности находится вне правой границы отсечения (или вне верхней границы), левый верхний квадрант расположен над верхней границей отсечения, подобным образом можно устранить оставшиеся два октанта.

Расчет точек пересечения включает подстановку точки на границе отсечения {хюцпъ, жгутах, У^и,т\п или у1и_тах) в нелинейное уравнение границы объекта и вычисление значения другой координаты. После того как все точки пересечения будут вычислены, положение определяющих точек объекта можно записать для дальнейшего использования в процедурах закрашивания по строкам развертки. На рис. 6.32 иллюстрируется окружность, обрезаемая прямоугольным окном. В данном примере радиус окружности и конечные точки отсекаемой дуги можно применить для закрашивания вырезанной области.

Подобные процедуры можно применить при обработке криволинейного объекта отсекающим многоугольником. При первом проходе алгоритма можно сравнить граничный прямоугольник объекта с граничным прямоугольником отсекающей области. Если это не позволит полностью записать или удалить объект, далее решается система уравнений кривых, из которой определяются точки пересечения с отсекающей фигурой.

⇐ вернуться назад | | далее ⇒