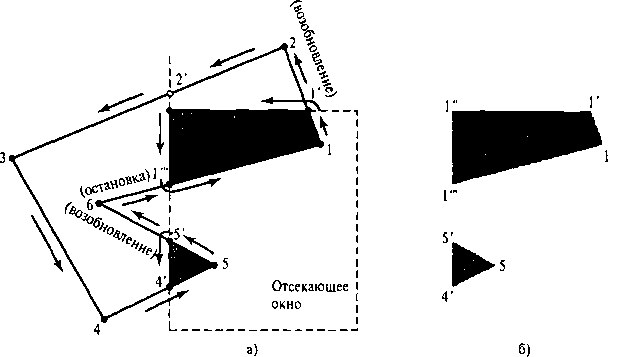
Рис. 6.29. Вогнутый многоугольник (панель о), определенный списком вершин {1,2,3,4,5.6}, при вырезании с использованием алгоритма Уэйлера-Азертона дает два списка {1,1', 1", 1"'} и {4', 5,5'}, представляющих два отдельных закрашенных многоугольника (панель 6)
2' и 3 - слева от отсекаемой области. Кроме того, сторона с конечными точками 3 и 4 расположена снаружи левой границы отсечения. Однако следующая сторона (от точки 4 до точки 5) снова входит в извлекаемую область, и нужно обработать точку пересечения 4'. Кроме того, сторона с концами 5 и 6 выходит из окна в точке 5', поэтому мы обходим снизу левую границу отсечения и получаем замкнутый список вершин {4', 5,5'}. Мы продолжаем обработку сторон многоугольника в точке 5', что возвращает нас к ранее обработанной точке 1'". В этой точке все вершины и стороны многоугольника обработаны, так что вся закрашенная область полностью извлечена.
ОБРАБОТКА МНОГОУГОЛЬНИКОВ С ИСПОЛЬЗОВАНИЕМ НЕПРЯМОУГОЛЬНЫХ ОТСЕКАЮЩИХ ОКОН
Алгоритм Лианга-Барски и другие параметрические методы отсечения линий особенно хорошо подходят для обработки многоугольных закрашенных областей с помощью отсекающих окон в форме выпуклых многоугольников. В этом подходе используется параметрическое представление сторон закрашенной области и отсекающего окна, и оба многоугольника представляются списком вершин. Вначале сравниваются положения прямоугольников, ограничивающих закрашенную область и отсекающий многоугольник. Если закрашенную область невозможно назвать полностью внешней по отношению к отсекающему многоугольнику, можно использовать проверки “внутри-снаружи” для обработки параметрических уравнений сторон. После проверки всех областей решаются системы параметрических уравнений линий, и определяются точки пересечения с окном.
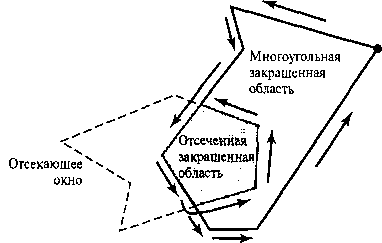
Рис. 6.30. Обработка многоугольной закрашенной области отсекающим окном в форме вогнутого многоугольника с использованием алгоритма Уэйлера-Азертона Любую многоугольную область можно также обработать любым отсекающим окном в форме многоугольника (выпуклого или вогнутого), как показано на рис. 6.30, используя схему обхода сторон (алгоритм Уэйлера-Азертона). В этом случае необходимо поддерживать для отсекающего окна и многоугольной области списки вершин, упорядоченные против часовой стрелки или по ней. Кроме того, нужно применить проверки “внутри-снаружи”, чтобы определить, находится вершина закрашенной области внутри или снаружи определенной границы отсекающего окна. Как и в предыдущем примере, границы окна прослеживаются, и определяется, где сторона закрашенной области выходит из отсекающей границы. Данный метод отсечения можно также использовать, если закрашенная область или отсекающее окно содержит отверстия, определенные многоугольными границами. Кроме того, данный базовый подход в конструктивной блочной геометрии используется для определения объединения, пересечения или разности двух многоугольников. Фактически вычисление отрезанной области закрашенной фигуры равнозначно определению пересечения двух плоских областей.
