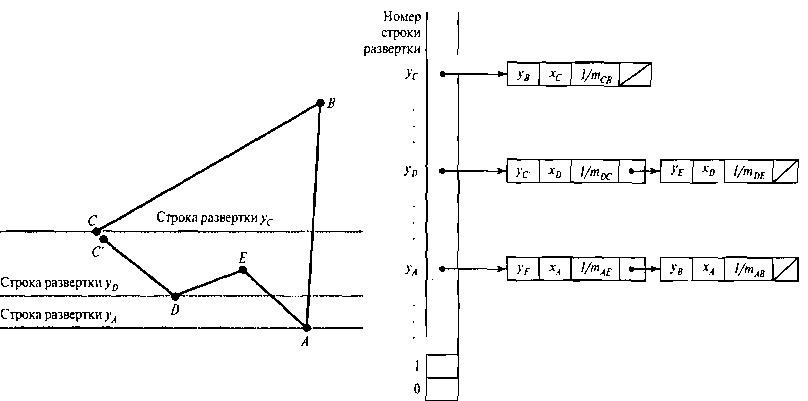
Рис. 4.24. Многоугольник и его сортировочная таблица сторон, где сторона ОС уменьшена на одну единицу в направлении у ваться блочной сортировкой и записать в нужных точках строки развертки стороны, отобранные по наименьшему значению у для каждой стороны. В сортировочную таблицу сторон заносятся только негоризонтальные стороны. После обработки можно также сократить определенные стороны, чтобы определиться с количеством вершин и точек пересечения. В каждой входной позиции таблицы для определенной строки развертки содержится максимальное значение у для этой стороны, значение х (в нижней вершине) и величина, обратная тангенсу угла наклона. Для каждой строки развертки стороны отсортированы слева направо. На рис. 4.24 показан многоугольник и соотнесенная с ним таблица сторон.
Далее мы обрабатываем строки развертки, начиная с нижней части многоугольника до верхней, создавая для каждой строки развертки, пересекающей границы многоугольника, активный список сторон. В активном списке сторон для строки развертки содержатся все стороны, пересекающиеся с этой строкой развертки, а также результаты итеративных расчетов, которые используются для поиска точек пересечения со сторонами.
Поиск точек пересечения можно упростить, записывая значения Дх и Ду в сортировочную таблицу сторон. Чтобы убедиться, что внутренние области заданного многоугольника закрашены правильно, можно воспользоваться рассуждениями, которые приводятся в разделе 3.13. Для каждой строки развертки закрашивается полоса пикселей между каждой парой отрезков координаты х, начиная с крайнего слева значения отрезка х и заканчивая в точке, предшествующей крайнему справа отрезку х. Кроме того, каждую сторону многоугольника можно сократить на одну единицу в направлении у в верхнем конце отрезка. Такие меры гарантируют, что пиксели, принадлежащие соседним многоугольникам, не будут накладываться друг на друга.
ПОСТРОЧНОЕ ЗАКРАШИВАНИЕ ВЫПУКЛЫХ МНОГОУГОЛЬНИКОВ
Информация о погоде в Чернигове за сегодня.
При применении процедуры построчного закрашивания к выпуклому многоугольнику каждой строке развертки не может соответствовать более одной внутренней полосы пикселей. Поэтому стороны многоугольника нужно обрабатывать только до тех пор, пока не будут найдены две точки пересечения границы многоугольника с каждой строкой развертки, проходящей через внутреннюю область многоугольника.
Общий вид растрового (построчного) алгоритма заполнения многоугольников, который рассматривался в предыдущем разделе, значительно упрощается, если нужно заполнить выпуклый многоугольник. Снова воспользуемся координатной областью и определим, какие стороны пересекает строка развертки. Затем путем поиска точек пересечения с этими сторонами найдем внутренние полосы пикселей для этой строки развертки, причем любая вершина, через которую проходит строка развертки, считается за одну точку пересечения с границей многоугольника. Если строка развертки проходит через одну вершину (например, через вершину многоугольника), мы наносим только эту точку. В некоторых графических пакетах существует более строгое ограничение: все закрашиваемые фигуры должны быть треугольниками. Данное условие еще больше упрощает процесс закрашивания, поскольку каждый треугольник состоит только из трех сторон, которые нужно обрабатывать.
