ОБЩИЙ ВИД РАСТРОВОГО АЛГОРИТМА ЗАКРАШИВАНИЯ МНОГОУГОЛЬНИКОВ
Растровое закрашивание участка выполняется следующим образом: сначала находятся точки пересечения границ закрашиваемой области со строками развертки экрана. Затем к каждому участку строки развертки, который лежит внутри закрашиваемой области, применяются цвета заполнения. В растровом алгоритме внутренние области определяются по тому же принципу, что и при применении правила четного-нечетного (раздел 3.15). Самой простой фигурой для закрашивания является многоугольник, поскольку каждая точка пересечения строки развертки с границей многоугольника находится при решении системы двух линейных уравнений, причем уравнение строки развертки записывается просто как у = const.
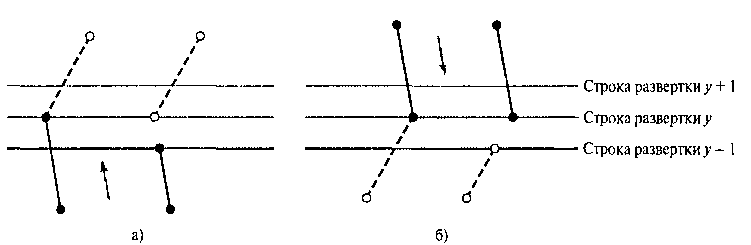
Рис. 4.22. Подбор значений координаты у концов сторон многоугольника при обработке периметра многоугольника. Сторона, которая обрабатывается в данный момент, показана сплошной линией. На панели а координата у верхнего конца текущей стороны уменьшается на 1. На панели б координата у верхнего конца следующей стороны уменьшается на I
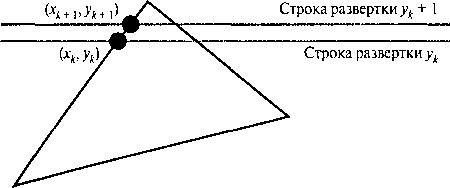
Рис. 4.23. Две соседние строки развертки, пересекающиеся с границей многоугольника Один из способов согласования количества вершин и точек пересечения - это сократить некоторые стороны многоугольника, чтобы отделить те вершины, которые следует считать как одну точку пересечения. Негоризонтальные стороны вокруг границы многоугольника, например, можно обрабатывать либо по часовой стрелке, либо против нее. При обработке каждой стороны можно проверять, будут ли значения координаты у концов этой стороны и следующей за ней монотонно увеличиваться или уменьшаться. Если да, тогда нижнюю сторону можно укоротить, чтобы получалась только одна точка пересечения со строкой развертки, проходящей через общую вершину, в которой соединяются эти две стороны. Пример такого укорачивания стороны показан на рис. 4.22. Если координаты у концов двух сторон увеличиваются, тогда значение координаты у верхнего конца текущей стороны уменьшается на 1, как показано на рис. 4.22, а. Если же значения координаты у концов сторон монотонно уменьшаются, как на рис. 4.22, б, тогда мы уменьшаем значение координаты у верхнего конца стороны, следующей за текущей стороной.
Как правило, определенные свойства одной части сцены некоторым образом связаны со свойствами других частей сцены, и эту когерентность можно использовать в алгоритмах компьютерной графики для сокращения числа выполняемых операций. Когерентные методы часто содержат в себе операции вычисления приростов, которые применяются к одной строке развертки или между соседними строками развертки.
Например, при определении точек пересечения со сторонами закрашиваемой фигуры можно вычислять прирост координаты вдоль какой-либо стороны, учитывая, что тангенс угла наклона стороны сохраняется при переходе от одной строки развертки к следующей.
Для эффективного закрашивания многоугольников сначала можно записать границы многоугольника в сортировочную таблицу сторон, в которой содержится вся информация, необходимая для эффективной обработки строк развертки. Перемещаясь по сторонам в направлении по часовой стрелке или против нее, можно воспользо-
