В общем случае временные затраты при использовании иерархий составляют 0(\о%п), где п - общее число объектов в иерархии.
Ниже приводится пример кода, осуществляющего проверку на пересечение заданного объекта с иерархической структурой в виде ВУН.
Рис. 3.18
bool checkBvhNode ( BvhNode * node, Object * object ) {
if ( lobject -> getBoundingBox ((.intersect ( node -> getBoundingBox () ) )
return false;
if ( node -> isLeaf () )
return node -> checkObject ( object );
for ( int i = 0; i < node -> getNumChildren (); i++ ) if ( node -> getChild ( i ) != NULL ) if ( checkBvhNode ( node -> getChild ( i ), object ) ) return true;
return false;
}Еще одним из вариантов дерева являются восьмеричные деревья (octree). В таком дереве каждый узел содержит до восьми потомков, которые строятся путем разбиения ограничивающего тела данного узла на 8 равных частей и определения объектов, содержащихся в каждой из таких частей.
Далее мы подробно рассмотрим BSP-деревья, работу с ними и их построение. На прилагаемом к книге компакт-диске содержится исходный код для построения и работы с восьмеричными и одним из вариантов BSP-деревьев - kd-деревьями.
Для работы с различными иерархическими структурами очень удобным оказывается паттерн "Посетитель" [12J.
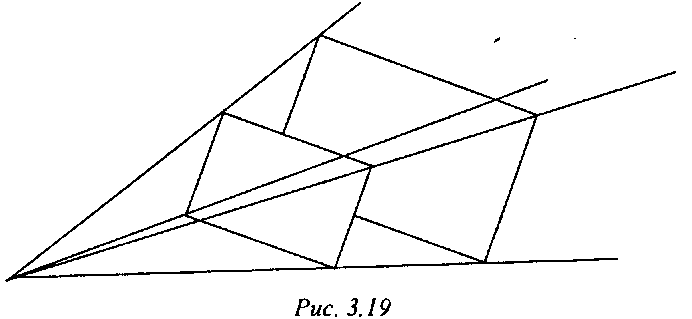
Область видимости Еще одним классом, который будет нам полезен в дальнейшем, является класс Frustrum, представляющий собой усеченную пирамиду (рис. 3.19).
Простейшие геометрические алгоритмы и структуры
Он задается ближней и дальней отсекающими плоскостями и набором плоскостей, проходящих через вершину пирамиды. Подобный объект очень удобен для моделирования области видимости наблюдателя и области пространства, видимой сквозь портал. Ниже приводится описание этого класса.
class Frustrum {
Vector3D org; // origin of frustrum
Vector3D vertices [MAX_VERTICES];
// these vertices and org make the frustrum int numVertices; Plane * farPlane;
Plane * nearPlane;