Рис. 3.15
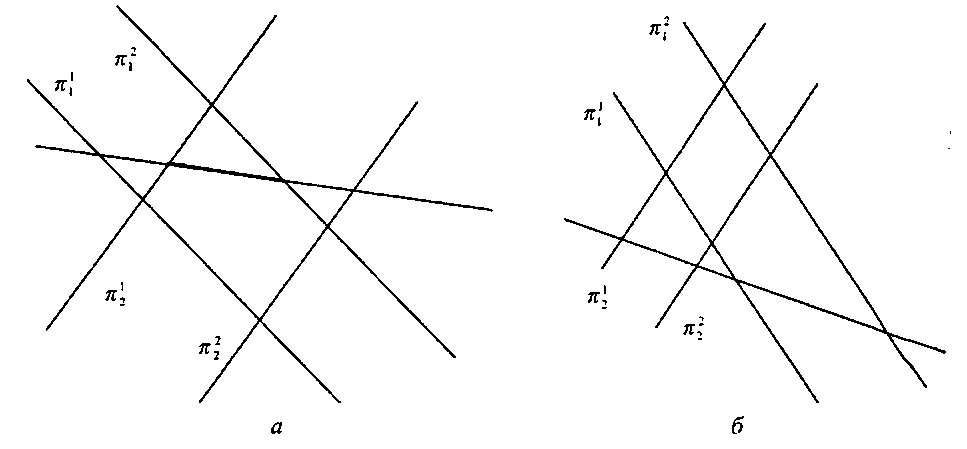
Простейшие геометрические алгоритмы и структуры
Проверка пересечения луча с многоугольником Еще одним часто встречающимся тестом является проверка луча на пересечение с заданным многоугольником. Первым шагом этого теста является проверка на пересечение луча с плоскостью, проходящей через этот многоугольник. Если пересечение имеет место, то находится его точка и проверяется принадлежность этой точки многоугольнику. Для этого достаточно спроектировать как сам многоугольник, так и проверяемую точку на одну из координатных плоскостей (обычно для минимизации численных по-фешностей выбирается плоскость, соответствующая наибольшей по модулю компоненте вектора нормали к многоугольнику). Таким образом, проверка сводится к двухмерному тесту принадлежности точки многоугольнику.
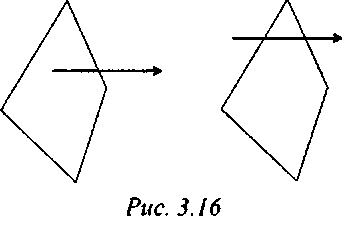
Эта задача обычно решается путем выпускания луча (на плоскости) из проверяемой точки Ii нахождения точек его пересечения с границей многоугольника. Пели оно нечетно (рис. 3.16), го точка лежит внутри, если нет -го снаружи.
В качестве направления выпускаемого луча можно взять произвольный ненулевой вектор, но обычно из соображений удобства выбирают направление одной из координатных осей. Определенная осторожность требуется при прохождении точки через вершину (см. [10]).
Ниже приводится код, осуществляющий подобную проверку.
в
'nool isPointlnside ( const Vector2D& p,
const Vector2D * v, int n )
bool inside = false;
Vector2D el ( v [0] ) ;
Vector2D eO ( v [n-1] );
bool yO = (eO.y >= p.y);
: or ( int i = 1; i < n; i++ )
{bool yl = (el.у >= p.y);
if ( yO != yl )
if ( (el.y-p.y)*(eO.x-el.x) >=
(el.x-p.x)*(eO.y-el.y)) == yl ) inside = !inside;уО = yl; еО = el; el = v [i];
}return inside; ч
} 'Проверка пересечения двух многоугольников Еще одной часто встречающейся задачей является проверка на пересечение двух выпуклых многоугольников. Ниже мы рассмотрим упрощенный случай пересечения двух треугольников.
Пусть заданы два треугольника ^(m^Mj) и Тг(у0УхУг) (лежащие в плоскостях я, и п2 соответственно) и необходимо определит пересекаются ли они.
