Удаление невидимых поверхностей
Пусть плоскость, производящая разбиение, задается уравнением
(p,n) = d.Каждый узел дерева можно представить в виде следующей структуры:
struct BSPNode
{
Plane plane; // splitting plane
Facet * facet; // corresponding facet
BSPNode * front; // left subtree
BSPNode * back; // right subtree
} ;где front указывает на вершину поддерева, содержащуюся в положительном полупространстве (p,n)>d, a back - на поддерево, содержащееся в отрицательном полупространстве (р, п)< d.
Обычно в качестве разбивающей плоскости выбирается плоскость, проходящая через одну из граней. Все грани, пересекаемые этой плоскостью, разбиваются вдоль нее, а получившиеся при разбиении части помещаются в соответствующие поддеревья.
Рассмотрим сцену, представленную на рис. 2.20. Плоскость, проходящая через грань 5, разбивает грани 2 и 8 на части 2', 2", 8' и 8", и все множество граней (с учетом разбиения граней 2 и 8) распадается на два кластера (1, 8', 2') и (2", 3, 4, 6, 7, 8"). Выбрав для первого кластера в качестве разбивающей плоскости плоскость, проходящую через грань 6, разбиваем его на два подкластера (7, 8") и (2", 3, 4). Каждое следующее разбиение будет лишь выделять по одной грани из оставшихся кластеров. В результате получим следующее дерево (рис. 2.21).
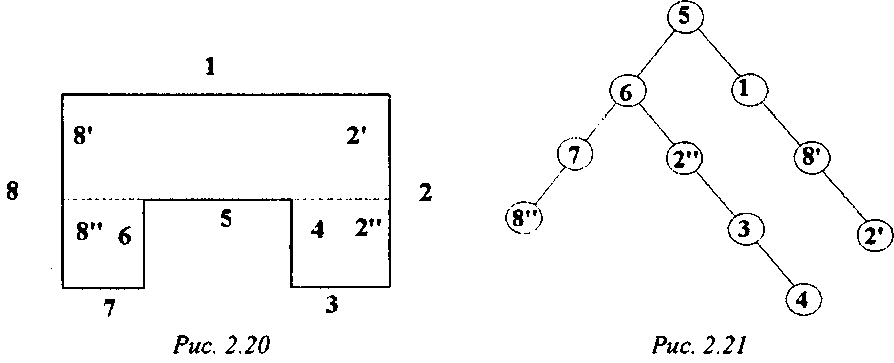
Таким образом, процесс построения В8Р-деревьев заключается в выборе разбивающей плоскости (грани), разбиении множества всех граней на две части (это может потребовать разбиения граней на части) и рекурсивного применения описанной процедуры к каждой из получившихся частей.
Замечание. Если проверяемая грань лежит в плоскости разбиения, то ее можно поместить в любую из частей. Существуют варианты метода, которые с каждым узлом дерева связывают список граней, лежащих в разбивающей плоскости.
Алгоритм построения ВБР-дерева очень похож на известный метод быстрой сортировки Хоара и его реализация может быть найдена на компакт-диске (или на сайте автора).
