Но здесь нужен механизм отслеживания того, какие пикселы были выведены, а какие нет. Для этого могут быть использованы самые разнообразные структуры, от линий горизонта до битовых масок.
Замечание Рассмотрим подробнее, каким именно образом осуществляются проверки тестов 3 и 4.
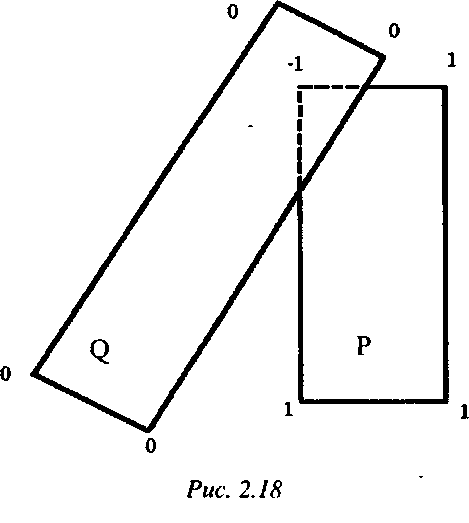
Пусть грань Р задана набором вершин Тогда для определения плоскости, проходящей через грань Р, достаточно знать вектор нормали л к этой грани и какую-либо ее точку, например А\. Уравнение плоскости, проходящей через грань Р, имеет следующий вид:
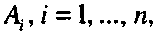
а грань О. - набором вершин
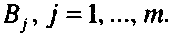
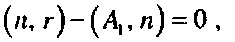
(2.5)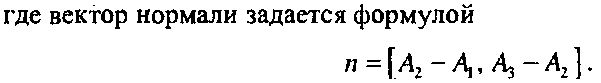
(2.6)Грань Q лежит по ту же сторону от плоскости, проходящей через грань Р, по которую располагается и наблюдатель, находящийся в точке V, если
sign{(n, В,)-(«, А)} = sign{(n, в)-(л, А)}, і = 1,т , (2.7)
и по другую сторону, если
sign[(n, В,)-(п, Al)} = -sign{(n, в)-(л, А)}.' = І.-, т . (2.8)
Метод двоичного разбиения пространства Существует другой, довольно элегантный и гибкий способ упорядочения граней.
Каждая плоскость в объектном пространстве разбивает все пространство на два полупространства. Считая, что эта плоскость не пересекает ни одну из граней сцены, получаем разбиение множества всех граней на два непересекающихся множества (кластера); каждая грань попадает в тот или иной кластер в зависимости от того, в каком полупространстве относительно плоскости разбиения эта грань находится.
Ясно, что ни одна из граней, лежащих в полупространстве, не содержащем наблюдателя, не может закрывать собой ни одну из граней, лежащих в том же полупространстве, в котором находится и наблюдатель (с небольшими изменениями это работает и для параллельного проектирования).
Для построения правильного изображения сцены необходимо сначала выводить грани из дальнего кластера, а затем из ближнего.
Применим предложенный подход для упорядочения граней внутри каждого кластера. Для этого выберем две плоскости, разбивающие каждый из кластеров на два подкласте-ра. Повторяя описанный процесс до тех пор, пока в каждом получившемся кластере останется не более одной грани (рис. 2.19), получаем в результате двоичное дерево (Binary Space Partitioning Tree - BSP). Узлами этого дерева являются плоскости, производящие разбиение.
