В случае, когда найденная точка пересечения сферы и плоскости принадлежит многоугольнику, она и является искомой точкой пересечения сферы с многоугольником.
В противном случае необходимо найти ближайшую к точке пересечения на сфере, найденной ранее, точку на границе многоугольника (рис. 8.6). Это и будет точка на многоугольнике, которая коснется сферы. После этого из этой точки выпускается луч в направлении, обратном к вектору скорости сферы. Если этот луч пересекает сферу, то пересечение имеет место и точкой пересечения на сфере будет точка ее пересечения с выпущенным лучом.
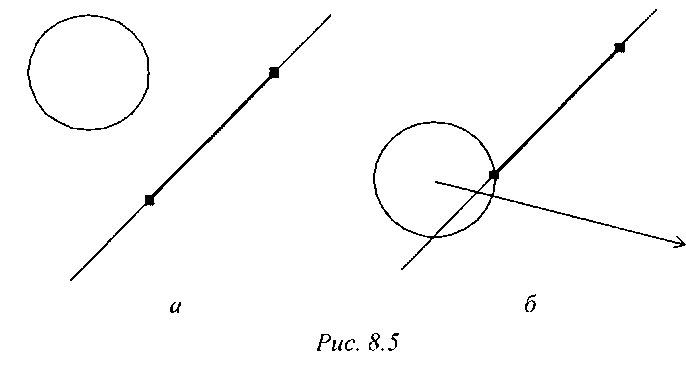
В противном случае (луч не пересекает сферу) пересечения сферы и многоугольника нет. Момент столкновения определяется параметром г пересечения выпущенного луча со сферой.
Рассмотрим теперь обработку столкновений. Обычно при столкновении объекта с гранью происходит скольжение объекта вдоль некоторой плоскости, проходящей через точку пересечения. Мы далее будем считать, что нормалью плоскости скольжения является нормаль к сфере в точке столкновения, что хорошо согласуется с физическим смыслом (рис. 8.7).
Таким образом после определения столкновения строится плоскость скольжения и вектор скольжения. После этого движение продолжается в направлении вектора скольжения.
строительство и недвижимость https://vishivka-krestikom.ru/.
Тем самым обработка столкновений носит рекурсивный характер - находится столкновение и, если оно имеет место, определяется вектор скольжения. После этого проверяется столкновение при движении из уже найденной точки столкновения вдоль вектора скольжения. Это может привести к новым столкновениям и скольжениям и т. д.
Рассмотрим теперь, как работать с объектами, не представляющими собой единичные сферы. В ряде случаев оказывается вполне оправданным представлять наблюдателя (для целей определения и обработки столкновений) как эллипсоид с осями, параллельными осям координат сцены. Непосредственная модификация описанного выше метода в общем случае эллипсоида довольно сложна, но этот общий случай может быть легко сведен в уже рассмотренному. Для этого достаточно применить преобразование масштабирование как к эллипсоиду, так и к проверяемым граням, в результате которого эллипсоид перейдет в единичную сферу. После этого осуществляется проверка пересечения единичной сферы с масштабированными многоугольниками и полученная точка пересечения масштабируется обратно с систему координат сцены.