Рассмотрим теперь, каким образом можно определять и обрабатывать столкновения наблюдателя с гранями сцены.
Сначала мы будем считать, что наблюдатель представляет собой единичную сферу, и рассмотрим определение столкновений с одной плоскостью (рис. 8.2, я).
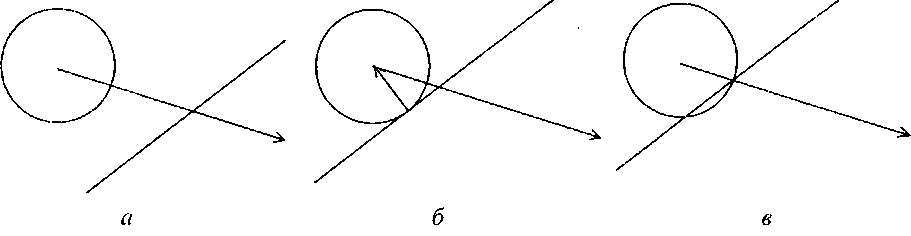
Рис. 8.2
В данном случае на рис. 8.2, в показано неправильное определение точки столкновения, а на рис. 8.2, б - правильное.
Для правильного определения столкновений единичной сферы с плоскостью прибавим к центру сферы О единичный вектор, направление которого противоположно направлению нормали к плоскости (-л) (рис. 8.3).
В результате мы получим точку на поверхности сферы, которая в результате движения коснется плоскости
Psph=0-n. (8.1)Из этой точки мы начинаем движение в направлении вектора скорости v. Выпустим из точки пересечения на сфере psph луч в направлении вектора скорости v. Этот луч описывается уравнением
P = P>rh+t-v. (8.2)Для определения момента этого столкновения можно воспользоваться методом intersectByRay класса Plane.
Vector3D spherelntersectionPoint =source - plane -> n;
plane --> intersectByRay ( spherelntersectionPoint,
normalizedVelocity, t ) ;
Vector3D pointOnPlane ( spherelntersectionPoint +
t * normalizedVelocity );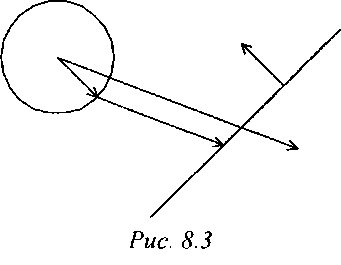
Пишем портальный рендерер (часть II)
Однако при этом желательно учесть случай, когда плоскость уже пересекает сферу, т. е. точка касания р к лежит в отрицательном полупространстве относительно плоскости (рис. 8.4).
В этом случае мы будем искать точку не в направлении вектора движения, а в направлении, обратном направлению вектора нормали к плоскости.
В результате описанного алгоритма мы определяем момент пересечения (параметр г), а также точку на плоскости, в которой произойдет столкновение.
Если у нас имеется набор плоскостей, то необходимо проверить на столкновение каждую из них. После этого выбирается ближайшая точка (соответствующая минимальному значению параметра г).
Столкновение сферы с многоугольником несколько сложнее (рис. 8.5, я). Для начала определяется пересечение сферы с плоскостью, проходящей через этот многоугольник. Проблема здесь заключается в том, что найденная точка столкновения сферы с плоскостью грани может и не принадлежать многоугольнику (рис. 8.5, б).
