v' = q-[0,V]q-1. (1.57)При этом если q = [cos 0, и sin 0], то поворот осуществляется вокруг оси, задаваемой вектором и на угол 29.
Последовательность поворотов соответствует произведению кватернионов, задающих эти повороты.
p{q[0,v]q'iyp-l=(pq)[0,v]ipqy1. (1.58)Из этого следует, что для поворота вектора на угол 9 вокруг вектора и следует использовать следующий кватернион:
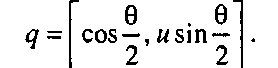
(1.59)Обратите внимание, что как кватернион <? = [и\ у], так и кватернион q = [-и-, - у] соответствуют одному и тому же повороту.
Координаты и их преобразования
Для заданного единичного кватерниона ц можно построить матрицу 3x3, соответствующую данному повороту.
'1-2(у2 + г2) 2{ху-ъг) 2{хг + щ) " М{а)= 2(ху + н>г) 1-2(д:2 + г2) 2{уг-м»х) . (1.60)
2(хг-ыу) 2(уг + ых) 1-2(л:2 + у2)
Также можно по заданной ортогональной матрице М построить соответствующий кватернион. Для этого из (1.57) достаточно выразить (и-, х, у, г) через элементы матрицы.
Для этого заметим, что сумма диагональных элементов матрицы (ее след) ггМ всегда равна Зи>2, откуда легко находится величина и>.
Далее производится вычитание элементов, симметричных относительно главной диагонали, друг из друга для получения мнимой части кватерниона, например
т1Л-тгл=-Аш- (1.61) Отсюда легко находится величина г.
Таким образом, для определения кватерниона по ортогональной матрице можно использовать следующие формулы:
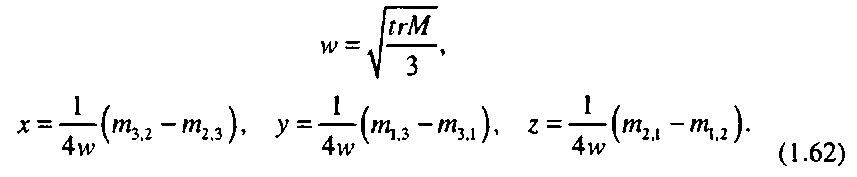
Для корректного применения формул (1.59) требуется, чтобы и>*0. Обычно из соображений численной устойчивости требуют, чтобы |и>|>е. Если это не выполнено, то считаем и> = 0. Тогда
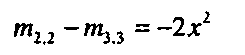
(1.63)в силу того, что строящийся кватернион является единичным. Отсюда находится х и проверяется выполнение условия |л:| > е . Если оно выполнено, то
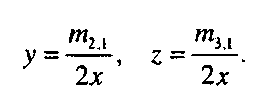
(1.64)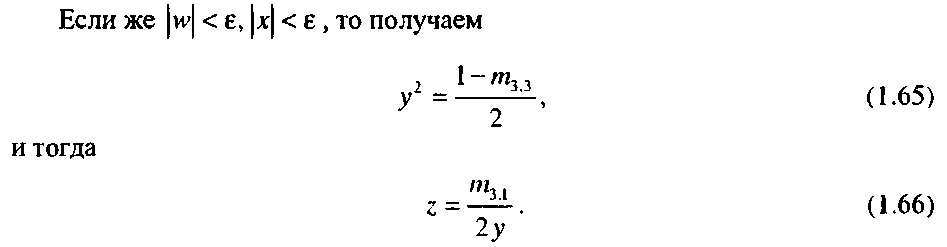
В противном случае считаем w = х = у = 0, z = 1 .
Часто возникает задача плавного перехода от одной ориентации к другой. Если обе эти ориентации заданы при помощи кватернионов, то для получения промежуточных ориентации удобно использовать так называемую сферическую интерполяцию кватернионов (slerp).
