При работе с объектами в трехмерном пространстве постоянно возникает задача задания ориентации объекта.

Одним из способов задания ориентации является задание при помощи ортогональной матрицы, однако такой способ очень неудобен, поэтому обычно используются другие способы.

Одним из самых простых способов задания ориентации объекта является использование так называемых углов Эйлера - именно Эйлером впервые было наказано, что из одной произвольной ориентации в трехмерном пространстве можно перейти в любую другую при помощи не более трех поворотов. Для этого выбираются три оси. Обычно в качестве этих осей выбирают отрицательное направление оси Ог и оси Ох и Оу (рис. 1.7).

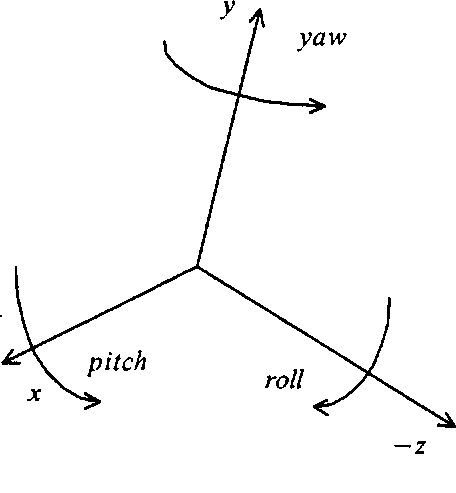
Рис. 1.7

Тогда произвольная ориентация может быть задана при помощи последовательных поворотов вокруг каждой из этих осей.

R(y,p,r)=R_"images/tmpFE1D-26.png">
Тогда для нахождения углов Эйлера можно воспользоваться следующим фрагментом кода: У1


pitch = asin ( r21 );
if ( pitch < M_PI / 2 ) {
if ( pitch > -M_PI / 2 ) {
roll = -atan2 ( -rOl, rll ); yaw = atan2 ( -r20, r22 );
}
else
{
roll = atan2 ( ro2, rOO ); yaw = 0;
}
}


Глава I. Координаты и их преобразования




else
{
roll = atan2 ( ro2, rOO ) ; yaw = 0;
}


Однако при использовании углов Эйлера может произойти неприятное явление, называемое gimbal lock. При этом происходит потеря одной из имеющихся степеней свободы.


Рассмотрим, например, случай, когда /? = ^ . В этом случае матрица поворота (1.38) примет следующий вид: Таким образом, матрица поворота (140) зависит только от суммы двух углов и одна степень свободы была утеряна, т. е. поворот вокруг оси Оу приведет к кому же, к чему приводит и поворот вокруг оси -Ог на тот же угол.




⇐ Предыдущая| |Следующая ⇒