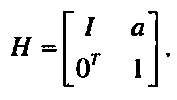
(1.24)Таким образом, произвольное аффинное преобразование в трехмерном пространстве у = Мх + а (1.25)
можно, используя матрицы однородных преобразований, записать в следующем виде:
(1.26)Если есть однородная матрица аффинного преобразования Н, то обратное преобразование определяется следующей матрицей:
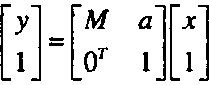
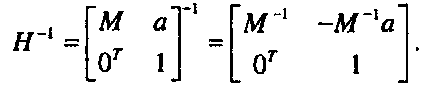
(1.27)Одним из преимуществ записи аффинных преобразований через однородные матрицы заключается в том, что суперпозиции преобразований соответствует перемножение соответствующих матриц. Обратному преобразованию соответствует обратная матрица.
Системы координат
Одна и та же точка в трехмерном пространстве может быть задана при помощи различных систем координат, и поэтому часто возникает необходимость перехода от одной системы координат к другой.
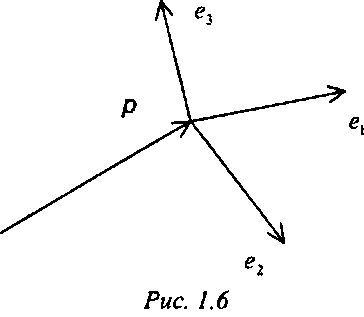
Система координат в трехмерном пространстве определяется своим началом р и тремя базисными линейнонезависимыми векторами е1, е2 и еъ (рис. 1.6). Далее эти векторы мы будем считать ортонормиро-ванными (т. е. их длины равны единице и они ортогональны друг другу). Базисные векторы е{,е2 и еъ можно записать как столбцы матрицы

В силу ортогональности базисных векторов еге2 и еъ матрица (1.28) является ортогональной, т. е. обладает следующими свойствами:

Координатная система называется правосторонней, если д&\ /? = 1, и левосторонней, если й&х /? = -1.
Базисные векторы правосторонней системы кординат удовлетворяют следующим соотношениям: е1=е1хе3, е2 = е3хег е} = е2хеу (1-31)
В стандартной системе координат
/> = (0,0,0)г, е,=(1,0,0)7, е2=(0,1,0)г, е3=(0,0,1)г. (1.32)
Если заданы координаты вектора х в одной системе координат, то можно получить его координаты х' в другой системе координат. Его координаты {х[, х2, х'ъ )Г удовлетворяют следующим соотношениям: х = р + х[е{ +х'2е2+ х'ъеъ = р + Их'. (1.33)
Координаты и их преобразования
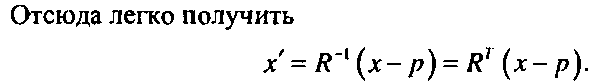
(1-34)Тогда для перевода в новую систему координат можно использовать однородное преобразование, задаваемое следующей матрицей:
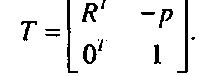
(1.35)Задание ориентации
