Н» V = (XV V + и V = ОСУ V.

Тогда

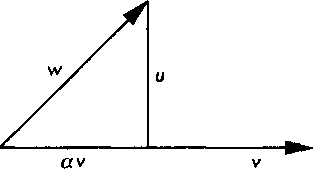
Рис. Б. 7. Проекция вектора на другой вектор

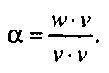
Вектор аг называется проекцией вектора м на вектор V. Второе слагаемое разложения вектора »г определяется соотношением

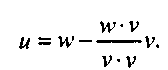
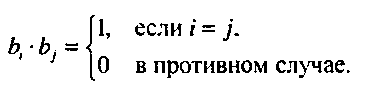
Полученный результат можно распространить на разложение вектора по ортогональным векторам произвольного базиса.

Б.6. Ортогонализация Грама-Шмидта Если в л-мерном пространстве определено множество векторов базиса аь а2,а,„ то в нем можно определить другой базис, оь Ь2,Ь,„ который будет ортонорлшрованным, т.е. каждый вектор этого базиса имеет единичную длину и ортогонален всем другим векторам базиса. Математически это выражается следующим образом"opengl5_602.html">⇐ Предыдущая| |Следующая ⇒