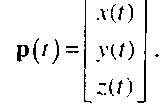
В исходном массиве данных имеются компоненты вектора скорости в этой точке:
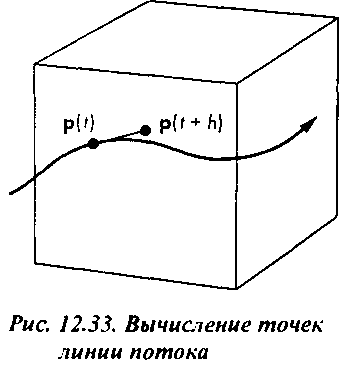
(')=К(о Если поместить мысленно в эту точку материальную частицу, то через небольшой интервал времени, т.е. в момент / + И, эта частица будет примерно в точке р(/ + И) = р(/) + Av(/), как показано на рис. 12.33. Эта точка- следующая на траектории движения частицы. Если поток стационарный, то эта точка также принадлежит линии потока р(/).
Новая точка будет лежать в одной из ячеек, образованных сеткой дискретизации первичных измерений. Следующую точку траектории частицы можно вычислить по той же формуле, но подставив в нее данные из элемента исходного массива, ближайшего к только что сформированной точке, либо воспользовавшись билинейной интерполяцией данных первичных измерений.
Если известно, что поток нестационарный, то интервал h выбирается равным интервалу съема первичных данных и для вычисления следующей точки траектории берутся данные из очередного массива либо, если интервал между очередными измерениями не равен И, значение в момент t+h формируется с помощью линейной интерполяции.
Визуализация данных научных исследований
12.7. Визуализация тензорных полей Данные, характеризующие состояние тензорного поля в каждой точке объема, также являются распределенными в некоторой окрестности этой точки. Например, можно измерять напряжения в каждой точке конструкции, которые вызываются внешними силами. Напряжение в точке (х, у, г) описывается матрицей размера 3x3 (тензором ранга 2):
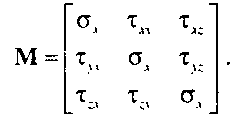
Диагональные члены матрицы представляют нормальные напряжения (силы, действующие на единицу площади), которые либо сжимают, либо растягивают материал по нормали к граням элементарного куба в данной точке. Члены матрицы, лежащие по обе стороны от диагонали, представляют силы, которые стремятся "перекосить" элементарный куб, превратить его в параллелепипед, как показано на рис. 12.34.
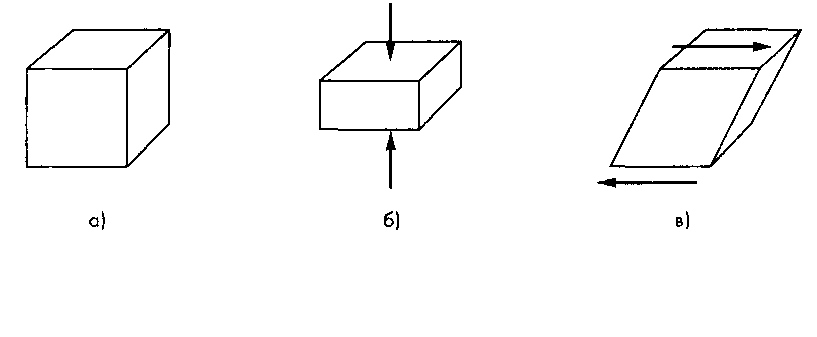
Рис. 12.34. Напряжения, действующие на элементарный куб конструкции: а - элементарный куб; б - нормальные напряжения; в - скашивающие напряжения
