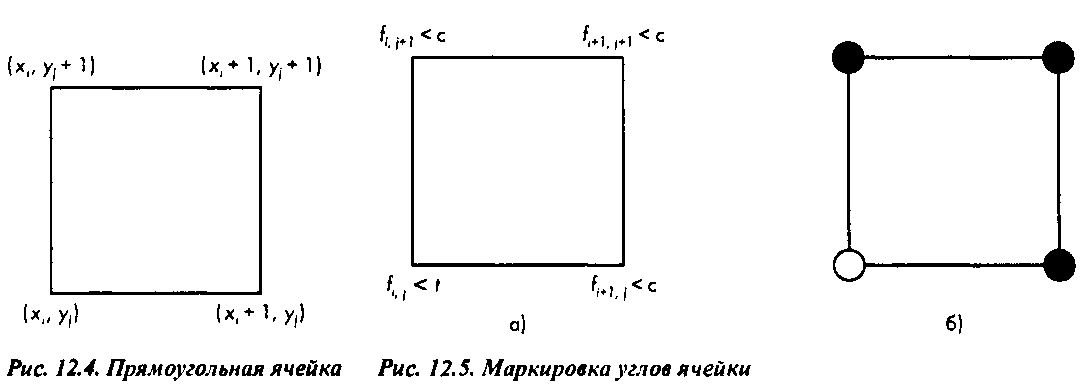
Рассмотрим простой случай, когда одно из значений в углах ячейки, скажем оказывается больше с, а значения в других углах - меньше с: Эту ситуацию можно схематически представить либо так, как на рис. 12.5,а, где соотношения для каждого узла выведены в виде надписей, либо так, как на рис. 12.5,6, где используется раскраска (маркировка) углов ячейки: белым цветом маркируется угол, в котором значение больше заданного, а черным - углы, в которых значения меньше заданного. Очевидно, что в этом случае кривая линии уровня должна пересечь два ребра ячейки, прилегающих к "белому" углу. Это же должно произойти и в том случае, когда значение в одном углу ячейки будет меньше с, а в соседних с ним - больше. Такая ситуация показана на рис. 12.6,а.
На рис. 12.6,а показано единственное пересечение ячейки линией уровня. Но возможен вариант, когда линия уровня пересекает ребро ячейки три раза (рис. 12.6,6), а в общем случае - любое нечетное число раз. Но мы всегда будем интерпретировать переход линии уровня через ребро ячейки как однократное, следуя одному из принципов Питера: если нечто можно объяснить по-разному, то самое простое объяснение будет и самым вероятным.
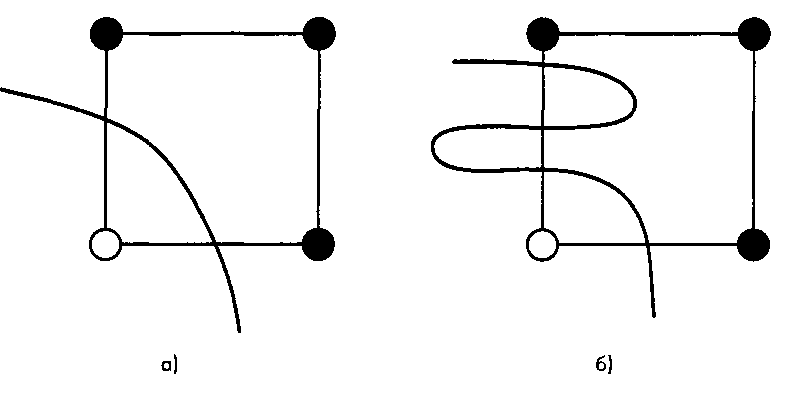
Рис. 12.6. Пересечение ячейки линией уровня: а - однократное; б - многократное
12.2. Поля превышений и линии уровня Если мы сможем оценить, в каких именно точках ребер линия уровня пересекает ячейку, то сможем соединить эти точки отрезком прямой и далее сразу вывести его на экран, поскольку анализ отдельных ячеек выполняется независимо. Но где установить точки пересечения? Тут возможны две стратегии. Можно просто установить точку пересечения на середине ребра между "белой" и "черной" вершинами. Но если значение а функции в вершине (х,,))) лишь незначительно больше с, а значение Ь в соседней вершине (х1+],у() значительно меньше с, то вполне резонно именно в таком отношении разделить ребро точкой пересечения. По такому принципу интерполируется положение точки пересечения с ребром. Рассмотрим, например, две соседние вершины ячейки, имеющие противоположную маркировку, т.е. значение функции в одной вершине больше с, а в другой - меньше с:
