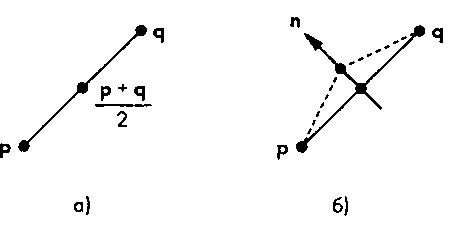
Рис. 11.24. Смещение средней точки: а - исходный линейный сегмент; б - сегмент после разбиения
Процедурные методы
пропорциональным / , где / - длина разделяемого сегмента, то результирующая кривая будет иметь размерность а1. Значение а!=\,5 соответствует траектории идеального броуновского движения.
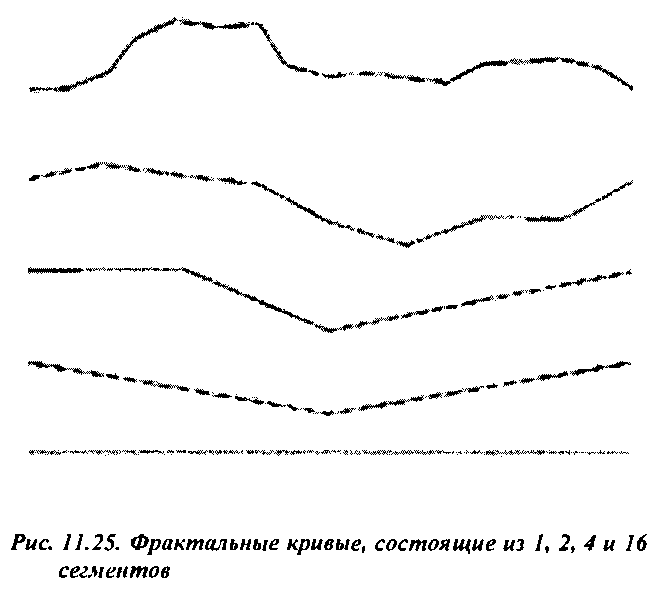
11.7.4. Формирование изображения горы с помощью фракталов В задачах компьютерной графики фрактальная технология получила наибольшее распространение при формировании деталей ландшафта, в частности гор. Для этого используется описанный выше метод рекурсивного разбиения в средней точке, но в качестве исходного объекта берется тетраэдр. Рассмотрим одну грань тетраэдра (рис. 11.26). Сначала определяются средние точки каждого из трех ребер грани. Затем каждая средняя точка смещается случайным образом. В результате формируется четыре новые треугольные грани. Управляя характеристиками генератора случайных чисел, задающего смещение, можно добиваться нужной степени мягкости или резкости рельефа горы. Обращаю ваше внимание на то, что к выбору характеристик генератора нужно отнестись очень внимательно, иначе результат не оправдает ваших ожиданий. Подробно об этом вы сможете узнать в специальной литературе, которая будет рекомендована для самостоятельного изучения в конце этой главы.
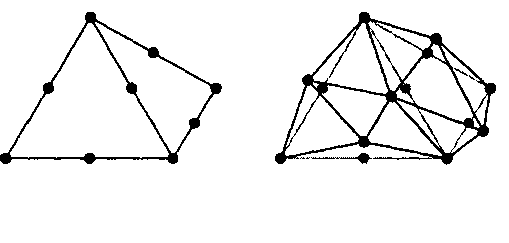
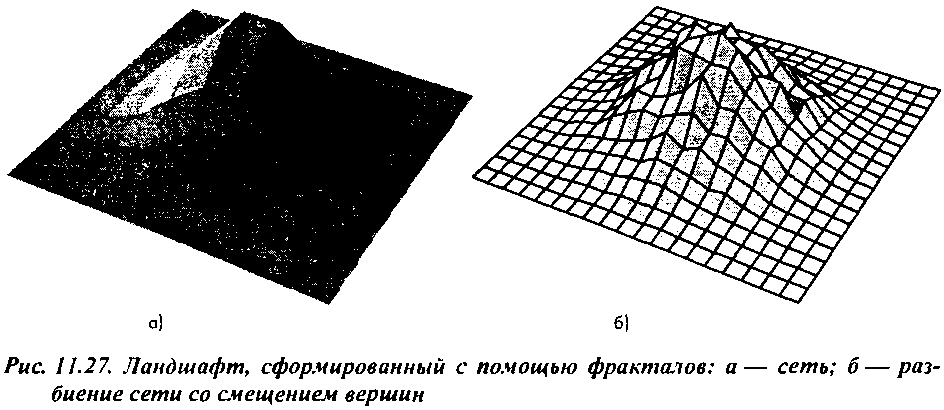
Рис. 11.26. Разбиение в средней точке граней тетраэдра Алгоритм разбиения в средней точке можно применять по отношению к любой полигональной сети. Можно начинать с плоской сети из четырехугольных ячеек в плоскости дг, г, а далее разбивать каждый четырехугольник на четыре более мелких и смещать все вершины случайным образом вверх (в направлении оси у). На рис. 11.27 показано, как выглядит промежуточный результат этого процесса.
11.7. Рекурсивные методы и фракталы
11.8. Множество Мандельброта Ни одно обсуждение темы фракталов, даже на самом элементарном уровне, не обходится без упоминания множества Мандельброта (Mandelbrot set). Хотя алгоритм формирования множества Мандельброта довольно прост, при этом формируются образы бесконечно сложной формы. Это множество является прекрасным примером использования таблицы соответствия цветов при генерации изображения. В дальнейшем изложении мы полагаем, что читатели знакомы хотя бы на самом элементарном уровне с арифметикой комплексных чисел.
