Сложнее всего обнаружить в модели столкновения сам факт столкновения. В игровых программах вполне достаточно приблизительно определить момент столкновения, и в таком случае можно заменить сложную модель геометрического объекта, состоящую из множества многоугольников, на один простой объект, например ограничивающий прямоугольник или параллелепипед. Обнаружить столкновение с таким каноническим объектом значительно проще.
Обращаю ваше внимание на то, что работа с точечными частицами позволяет избежать вычислений, которые обязательно пришлось бы выполнять, если бы анализировалось столкновение объекта определенной пространственной формы. Задача обнаружения столкновений во многом напоминает задачу отсечения одного объекта другим - хотя сами по себе формулы и не сложны, но объем вычислений оказывается значительным и на него уходит довольно много времени. Кроме того, при работе с объектами конечной формы нужно учитывать силы инерции, что повышает количество дифференциальных уравнений, описывающих состояние системы1. В компьютерной графике чаще всего используется приближенное решение системы уравнений, описывающей состояние системы, а потом на место идеальных частиц с точечной массой в изображение помещается какой-либо геометрический объект со своей формой и атрибутами.
Существует еще один вариант жестких ограничений, который часто включается в физическую модель, - учет сил контактного взаимодействия (contact forces). Предположим, что в модели имеется частица, на которую действует сила, толкающая ее параллельно какой-либо поверхности (рис. 11.9).
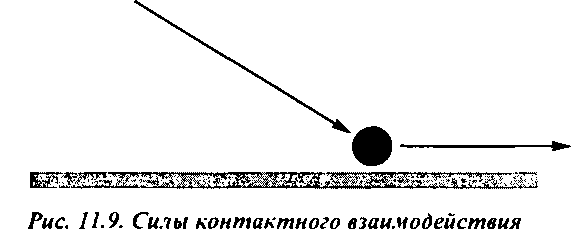
С одной стороны, под действием этой силы частица не может "проникнуть" в поверхность, а с другой - не должна и отрываться от нее. В такой системе следует учитывать только компоненту вектора суммарных сил, касательную к поверхности. Можно пойти дальше и включить в физическую модель еще и учет сил трения при движении вдоль поверхности.
11.5.2. Частицы внутри сферической оболочки Прежде чем перейти к анализу мягких ограничений, остановимся на время еще на одном жестком ограничении. Начнем с группы частиц, заключенных в сферическую оболочку радиуса /-, центр которой находится в начале координат. Предположим, что на частицы действуют силы взаимного отталкивания, величина которых обратно пропорциональна расстоянию между ними. Соударение частиц с поверхностью оболочки носит характер упругого столкновения. Пусть р,{() и у,(0 - положение и скорость /-й частицы в момент времени /. Расстояние а1,, между /-й иу'-й частицами равно
