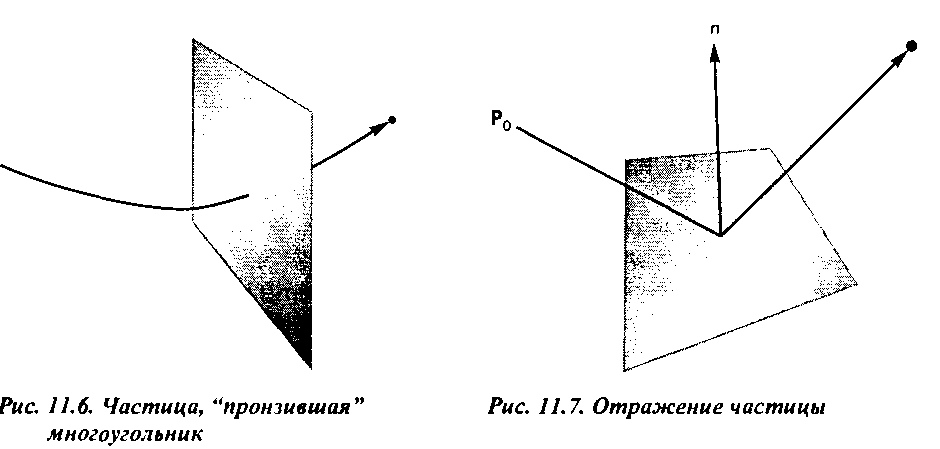
Пусть какая-либо частица пронизала многоугольник, как показано на рис. 11.6. Обнаружить сам факт столкновения частицы с многоугольником можно, подставив координаты положения частицы в уравнение плоскости многоугольника. Если временной шаг интегрирования уравнений состояния частиц достаточно мал, то, полагая, что скорость частицы на последовательных шагах изменяется незначительно, можно с помощью линейной интерполяции восстановить момент времени, когда в действительности произошло столкновение.
То, что происходит с частицей после столкновения, во многом напоминает то, что происходит со световым пучком после отражения. Если имеет место неупругое столкновение (inelastic collision), то частица не теряет энергии и ее скорость (точнее, модуль скорости) остается неизменной. Но направление движения изменится в соответствии с законом идеального зеркального отражения. Следовательно, если известны нормаль n к поверхности в точке столкновения s и предыдущая позиция частицы р, то можно вычислить угол идеального зеркального отражения по методике, описанной в главе 6 (рис. 11.7):
r=(2(p-s)-n)n-{p-s).Частица "пролетит" вдоль вектора отражения п такое же расстояние, как и то, которое она "проле тит", пронзив многоугольник, если бы столкновение не было обнаружено (рис. 11.8).
Направление движения изменится, а модуль вектора скорости останется прежним. Следовательно, та компонента вектора скорости, которая направлена вдоль плоскости многоугольника, остается неизменной, а компонента, параллельная нормали, меняет знак на противоположный.
Более сложным является механизм моделирования упругого столкновения (elastic collision), при котором частицы теряют часть своей энергии. Коэффициент восстановления {coefficient of restitntinn\ части и м - чтп тя чягть нппмяпкнпй кпм>
Глава П. Процедурные методы
поненты вектора скорости, которая сохраняется после столкновения. Следовательно, угол отражения вычисляется как и для неупругого столкновения, но нормальная компонента вектора скорости уменьшается в соответствии со значением коэффициента восстановления.
