Мы будем использовать этот объект для демонстрации применения метода рекурсивного разбиения, пользуясь уже известными вам средствами графической си^^мы OpenGL. Каждую порцию поверхности будем "пропускать" через п циклов разбиения и после этого формировать изображение по сформированному массиву вершин, используя либо отрезки прямых, либо многоугольники, проведенные через четыре угловые точки сформированной "микропорции". Следовательно, формирование на экране изображения микропорции можно выполнить с помощью следующей функции:
void draw_patch(point3 p[4][4j) {
glBegin(GL_QUADS);
glVertex3fv(p[0][0]);
glVertex3fv(p[3][0]);
glVertex3fv(p[3][3]);
glVertex3fv(p[0][3]); glEnd();
}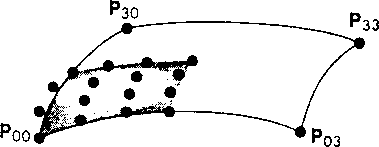
Рис. 10.38. Квадрант порции поверхности, образовавшийся посте разбиения
Кривые и криволинейные поверхности
Функцию разбиения порции образуем из функции разбиения сегмента кубической кривой Безье с, в которой используется ранее определенный тип данных point3.
void divide_curve(point3 с[4], point3 г[4], point3 1[4]) {
int i; point3 t; for(i=0;i<3;i++) {
l[0][i]=c[0][i];
r[3][i]=c[3][i];
l[l][i]=(c[l][i]+c[0][i])/2;
r[2][i]=(c[2][i]+c[3j[i])/2;
t[i]=(l[l][i]+r[2][i])/2;
l[2][i]=(t[i]+l[l][i])/2;
r[l][i]=(t[i]+r[2][i])/2;
l[3][i]=r[0][i]=(l[2][i]+r[l][i])/2;
}
}Рекурсивную программу разбиения порции поверхности несложно построить в виде последовательности вызовов функции divide_curve () и предполагая, что в нашем распоряжении имеется функция транспонирования матрицы transpose(). Текст этой программы приведен ниже.
void divide_patch(point3 р[4][4], int n) {
point3 q[4][4], r[4][4], s[4][4], t[4][4]; point3 a[4][4], b[4][4]; int i,j, k;
if(n==0) draw_patch(p); eise {
for(k=0; k<4; k++) divide_curve(p[k], a[k], b[k]); transpose(a); transpose(b); for(k=0; k<4; k++) {
divide_curve(a[k], q[k], r[k]); divide_curve(b[k], s[k], t[k]);
}
divide_patch(q, n-1); divide_patch(r, n-1); divide_patch(s, n-1); divide_patch(t, n-1);
}
}Полный текст программы формирования тонированного изображения чайника Юта вы можете найти на ftp-сервере по адресу ftp.cs.unm.edu в каталоге pub/angel/BOOK. В текст программы включен и массив координат исходных опорных точек, описывающих тестовый объект.
