P(0) = q(l)=7(p1_2+4p,_1+p,), о
p/(0) = q'(l)=|(pl-pl.2).Если выразить р(м) через массив коэффициентов с в виде р(г/) = и7с, то сформулированные условия примут вид С0=7(Р,-2+4Р,-. +Р,).
о с,=^(р,-р,-2).
Симметричные условия можно сформулировать для точки р(1): р(1) = с0 +с, +с2 +с3 =7(р,-, +4р, +р,+1), о р'(1) = с,+2с2+Зс3=|(р<+1-р,.1).
Теперь в нашем распоряжении имеется система четырех уравнений для коэффициентов с, которую можно решить, зная матрицу Ms- базисную матрицу В-сплайна (B-spline geometry matrix):
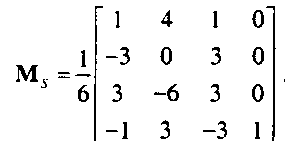
Значения элементов матрицы М.у определяют несколько интересных свойств полинома. Их несложно вывести, обратившись опять к полиномиальным функциям смешивания:
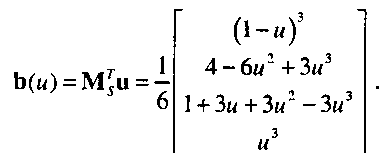
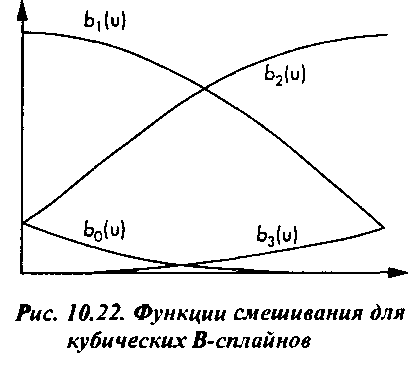
Графики этих функций показаны на рис. 10.22. Как и в случае с формой Безье, полиномиальные функции смешивания обладают следующими свойствами:
2>>) = 1 и 0 < Ь,(и) < 1 на интервале 0 < и < 1.
Кривые и криволинейные поверхности
Следовательно, сформированный сегмент кривой должен лежать в границах, заданных выпуклой оболочкой из опорных точек, как показано на рис. 10.23. Обратите внимание, что сегмент перекрывает только часть диапазона изменения параметра в пределах оболочки. Мы формулировали ограничения таким образом, чтобы составная кривая принадлежала к классу непрерывности С1, но фактически она относится к классу непрерывности10 С2. Это несложно проверить, вычислив значение р"(") в точках и=0 и и=1. Вы увидите, что эти значения одинаковы, а следовательно, сегменты справа и слева от точки сопряжения имеют разные значения вторых производных. Это свойство сплайновых кривых делает их особенно привлекательными для задач конструирования в интерактивном режиме.
Если по одному и тому же ансамблю опорных точек формировать сплайновую кривую, кривую Безье и составную интерполяционную кривую, то в первом случае приходится выполнить почти в три раза больше вычислений, чем в двух других. Это объясняется тем, что за один цикл вычислений при аппроксимации кривой сплайном формируется сегмент длиной, соответствующей расстоянию между соседними опорными точками, а во втором и третьем случаях длина сегмента в три раза больше.
