По этому же принципу при обработке набора {р,_3, р,_2, Р/_ь р,} строится сегмент между р,_2 и р,_ь а при обработке набора {р,_ь р„ Р/+ь Р/+2} - между точками р, и р,+,. Пусть р(и) - сегмент составной кривой между точками р,_1 и р„ а q{u) - сегмент кривой слева от него, между точками р,_2 и р,_). Можно сопоставить характеристики кривой в точке р(0) с характеристиками в точке я(1). Используя принятые ранее обозначения, будем искать матрицу М, которая обеспечит формирование искомого полинома в форме р(г/) = и7Мр, где р есть матрица опорных точек:
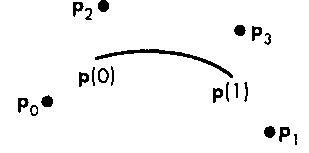
Рис. 10.21. Четыре опорные точки, определяющие сегмент В-сплайна
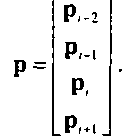
Аналогичное соотношение можно записать и для сегмента <\(и)"images/tmpB6CA-479.png">
В принципе можно было бы выписать набор ограничений, накладываемых на характеристики точки р(0) при их сопоставлении с характеристиками точки я(1), и такие же ограничения на характеристики точки р(1) при их сопоставлении с начальной точкой сегмента справа от него. Например, ограничение р(0) = Ч(1)
обеспечивает непрерывность составной кривой в точке сопряжения, но не требует, чтобы составная кривая проходила через какую-либо опорную точку. Это ограничение представляет собой одно из уравнений системы, решением которой являются элементы матрицы М. Очевидно, что можно придумать довольно много разных ограничений и получить в результате избыточную систему уравнений. Выбирая то или иное множество уравнений из этой избыточной системы, можно вычислить разные значения элементов матрицы М.
Можно ограничить пространство перебора и вычислить элементы матрицы для наиболее распространенного сочетания ограничений. Этот вариант строится исходя из того, что
10.7. Кубические В-сплайны
нам нужно использовать симметричную аппроксимацию в точке сопряжения сегментов. Следовательно, любая формулировка ограничений на характеристики в точке q(l) не может использовать опорную точку р,.3, поскольку она не может появиться в уравнении, которые мы выпишем для р(м). Точно так же, нельзя использовать р(+І в любом уравнении, составленном для характеристик точки р(0). Этим условиям симметричности будут соответствовать два уравнения:
