Следовательно, кривая р(и) должна лежать внутри выпуклой многоугольной оболочки, образованной четырьмя заданными опорными точками, как показано на рис. 10.18. Таким образом, оказывается, что хотя полиномиальная кривая Безье и не проходит через все заданные опорные точки, она никогда не выходит за пределы области, ограниченной этими точками. Эти два свойства кривых Безье, к которым следует еще присовокупить и возможность работать при конструировании таких кривых только с координатами опорных точек, определили широкое распространение этого класса кривых в практических приложениях компьютерной графики и в системах автоматизации проектирования. Пользователь может задать расположение четырех опорных точек, получить эскиз кривой, построенной на их основе, а затем, перемещая опорные точки, "подгонять" форму кривой.

10.6.2. Порции поверхности в форме Безье Порции поверхностей Безье (Bezier surface patches) можно сформировать с помощью функций смешивания. Если Р-[р(/] - массив опорных точек с размерами 4x4, то соответствующая порция поверхности в форме Безье описывается соотношением я з Р(«. v) = ££k (u)bl(v)p„ = urMflPM> .

i=0 7=0

Порция поверхности проходит через угловые точки роо, Роз, Рзо и Рзз и не выходит за пределы выпуклого многогранника, вершинами которого являются опорные точки (рис. 10.19). Двенадцать опорных точек из 16 можно интерпретировать как данные, определяющие направление производных по разным параметрам в угловых точках формируемой порции поверхности.

Рассмотрим, например, угол порции поверхности, соответствующий значениям параметров m=v=0. Можно рассчитать функцию р(м, 0) и первые частные производные от p(w, v) в этой точке следующим образом:

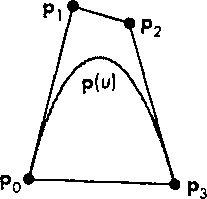
Рис 10.18. Выпуклая оболочка и полиномиальная кривая Безье

10.6. Кривые и поверхности в форме Безье

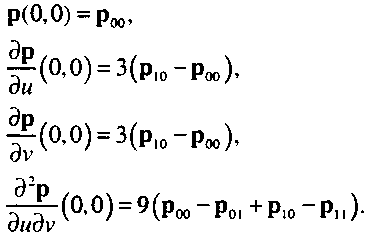
Первые три соотношения являются очевидными расширениями граничных условий, которые были сформулированы при анализе кривых Безье. Четвертое соотношение можно рассматривать как меру оценки тенденции порции поверхности в этой угловой точке к изгибу, отклонению от плоской формы - кручению (twist). Рассматривая четырехугольник, вершинами которого являются роо, Рт, Pi i и Роь придем к выводу, что кручение будет равно нулю только в том случае, если все точки лежат в одной плоскости. На ил. 8 цветной вклейки показано изображение рельефа, которое сформировано с использованием порций поверхностей Безье, построенных на основании массива данных об уровнях опорных точек рельефа.

⇐ Предыдущая| |Следующая ⇒