с = Мдр, где Мв называется базисной матрицей Безье (Bezier geometry matrix)9. Матрица Мй имеет вид
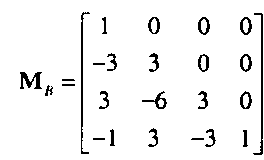
Следовательно, кубический полином Безье определяется соотношением р(г/) = и/Мдр.
Эту формулу можно использовать точно так же, как и аналогичную формулу для составной кривой, сегменты которой являются интерполяционными полиномами. Если имеется ансамбль опорных точек Ро,..,р„, то первую четверку ро, р|, р2 и рз будем использовать для определения первого сегмента составной кривой, конечную точку первого сегмента р3 и следующие три опорные точки р4, р5 и р6 - для определения второго сегмента и т.д. Очевидно, что составная кривая, построенная по методу Безье на произвольном ансамбле опорных точек, относится к классу С0 параметрических непрерывных кривых, но требованиям класса С1 она не удовлетворяет, поскольку касательные справа и слева отточки сопряжения аппроксимируются по разным формулам.
Важные свойства кривых Безье станут более понятными после анализа функций смешивания для этого класса кривых (рис. 10.17). Можно представить кривую в виде р(и) = Ь(м)7р, где
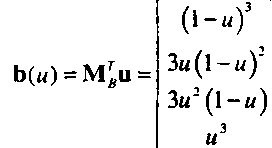
Эти четыре полинома являются частными случаями полиномов Бернштейна (Bernstein polynomials):
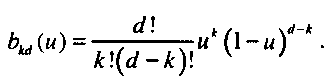
Полиномы Бернштейна обладают рядом интересных свойств. Во-первых, все нули полинома располагаются либо в точках и=0, либо в точках и=\. Следовательно, каждая полиномиальная функция смешивания удовлетворяет условию 0 < Ь1ски)щ>и 0<м<1. Поскольку полиномиальные функции не имеют нулей на интервале представления параметра, все они достаточно гладкие. Несложно показать, что на этом интервале полиномы Бернштейна удовлетворяют условиям (см. упр. 10.4)
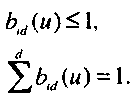
Иногда в литературе можно встретить название этой матрицы "базисная матрица кубической кривой Безье ". - Прим. ред.
436 Глава 10. Кривые и криволинейные поверхности Учитывая эти свойства полиномов Бернштейна, можно утверждать, что форма Безье кубической полиномиальной кривой является выпуклой суммой: з
р(и)=5^оор.
(=0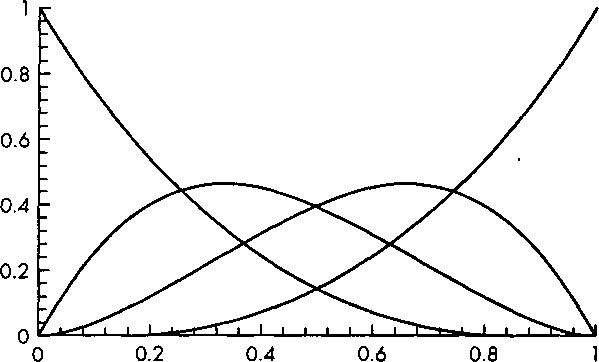
Рис. 10.17. Полиномиальные функции смешивания для кривых в форме Безье
