Теперь на время оставим задачу определения функции отображения и обратим взор на метод определения засветки пикселей. Одно из возможных решений - использовать точку, полученную при обратном отображении центра пикселя, и извлечь соответствующее значение функции окраски образца. Этот метод прост, но приводит к появлению на изображении дефектов квантования, которые особенно заметны в том случае, когда изображение образца носит периодический характер. На рис. 9.5 показано, в чем причина подобных искажений. На этом рисунке слева вы видите регулярную текстуру в виде полос, которую нужно наложить на плоскую поверхность. Обратная проекция центра каждого пикселя попадает как раз в промежуток между темными полосами, и в результате вся поверхность будет светлой. В общем случае, если не принимать во внимание конечные размеры пикселя, на изображении появится муар. Лучшие результаты можно получить другим методом (но его сложнее реализовать) - формировать возвращаемое значение интенсивности образца, усредняя значения интенсивности Т по области, обратной проекции пикселя. Этот метод дает лучший результат, но и он не идеален. Например, на рис. 9.6 показано, что происходит при его применении. На сей раз мы опять не получим на изображении полос, поскольку оно будет иметь усредненный цвет- ни светлый, ни темный. Таким образом, нам и на этот раз не удалось избавиться от дефектов, связанных с ограниченным разрешением буфера кадра и образца. Наиболее заметны эти дефекты при регулярной структуре образца текстуры.
Вернемся вновь к проблеме отображения одного пространства на другое. В компьютерной графике большинство криволинейных поверхностей задается в параметрической форме. Точка р на поверхности является функцией двух параметров и и V. Для каждой пары значений параметров формируется точка:
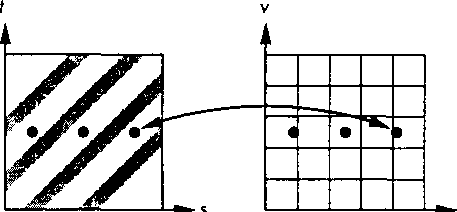
Рис. 9.5. Эффект дискретизации при наложении текстуры
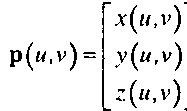
Процесс формирования параметрической поверхности мы более подробно рассмотрим в главе 10, а сейчас нас интересует, как отобразить точку в пространстве текстуры (5, /) на точку р(г/, г), принадлежащую такой поверхности. Рассмотрим линейную форму функции отображения"opengl5_419.html">⇐ Предыдущая| |Следующая ⇒
