Но при более внимательном взгляде обнаруживается множество "подводных камней". Во-первых, нужно определиться с методом сопоставления координат текстуры с геометрическими координатами. Двухмерный образец обычно определяется на прямоугольной области в пространстве текстуры. Функция отображения этого прямоугольника на область произволь2В четырехмерном случае значение текселя Т есть точка в пространстве (s. t, г, q/.

Операции с изображением на уровне растрового представления

ной формы в трехмерном пространстве может быть достаточно сложной или обладать нежелательными свойствами. Например, если желательно отобразить прямоугольную область на сферу, это невозможно сделать, не искажая форму образца или пропорции его компонентов (отношения между расстояниями). Во-вторых, сама организация процесса тонирования (он выполняется последовательным перебором пикселей) заставляет нас интересоваться скорее обратной функцией отображения, т.е. отображением координат экрана на координаты текстуры. Нас интересует при этом, какая точка на образце соответствует определенному пикселю образца поверхности, а это требует пересчета координат экрана в координаты текстуры. В-третьих, поскольку мы вычисляем коды засветки пикселей, каждый из которых определяет цвет элементарной прямоугольной области изображения, то нас интересует не функция отображения точки одного пространства на точку другого, а области в одном пространстве на область в другом. Здесь мы вновь сталкиваемся с проблемой сглаживания границ между областями, которой следует уделить особое внимание. В противном случае появляются совершенно неожиданные эффекты типа муара.

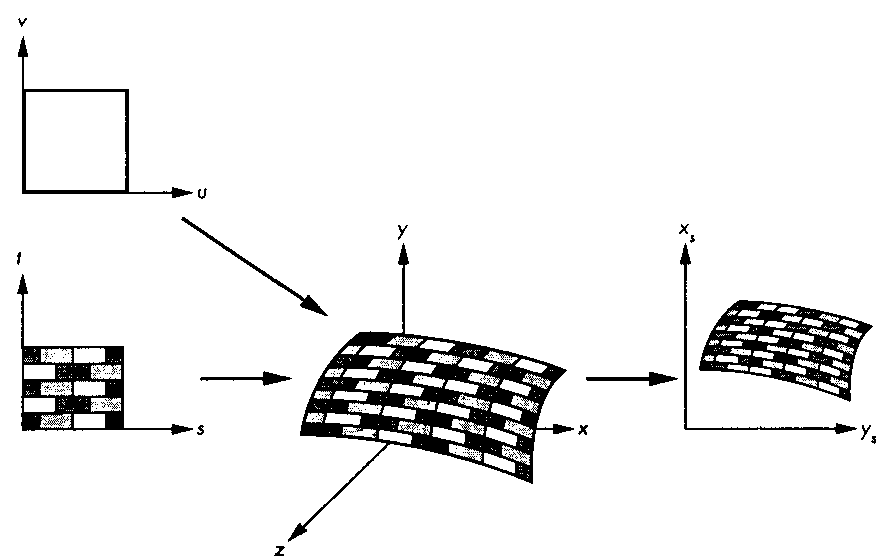
Рис. 9.3. Карты наложения при параметрическом задании поверхности

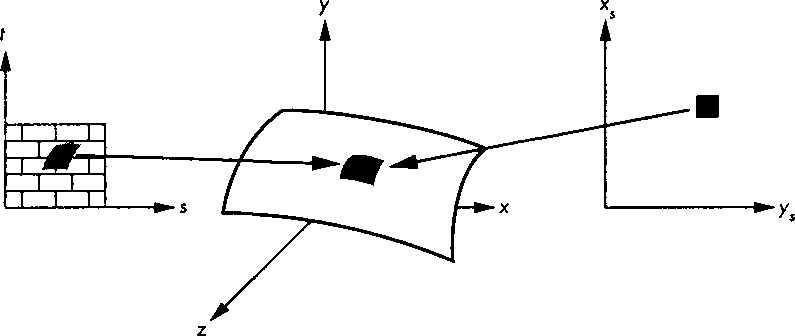
Рис. 9.4. Обратное отображение пикселя

9.2. Наложение проективных текстур

На рис. 9.4 схематически показана суть возникающих при наложении сложностей. Предположим, что вычисляется цвет квадратного пикселя, центр которого находится в точке (л"opengl5_418.html">⇐ Предыдущая| |Следующая ⇒