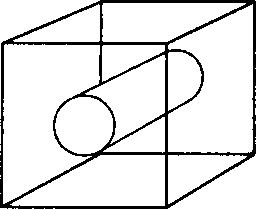
Рис. 8.20. Проволочное изображение объекта, которое может быть неоднозначно интерпретировано наблюдателем
объединение (union) двух множеств А н В, которое записывается в форме Ли В, - есть новое множество, включающее все элементы (точки) обоих исходных множества и В;
пересечение (intersection) множеств А и В (А п В) представляет собой множество всех точек, которые одновременно входят и в множество А, и в множество В;
операция вычитания множеств (set difference), А-В, формирует новое множество, состоящее только из тех точек множества/!, которые не принадлежат множеству В.
На рис. 8.21 показаны два исходных объекта и три объекта, сформированных из них разными операциями теории множеств.
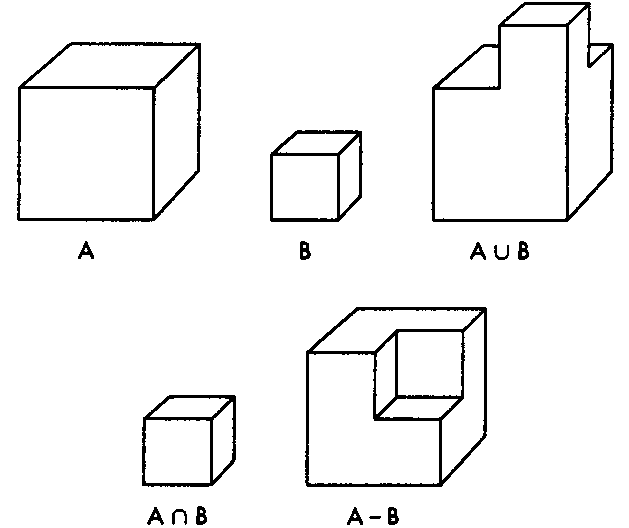
Рис. 8.21. Операции теории множеств
Иерархические графические модели
Эти операции описывают объекты, созданные из примитивов (или других объектов, созданных ранее из примитивов). На рис. 8.22 показаны четыре примитива и объект, описываемый выражением (А-В) п(Си £>).
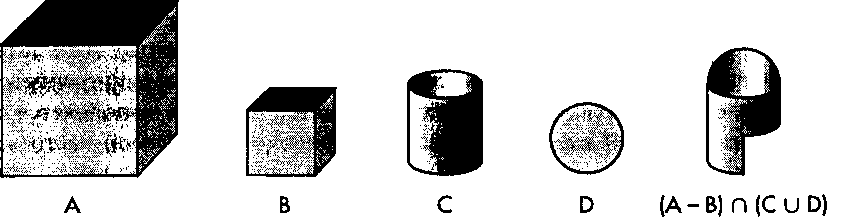
Рис. 8.22. Формирование объекта в конструктивной геометрии тел Как правило, для обработки алгебраических выражений используется дерево операций, внутренние узлы которого представляют операции, а терминальные - операнды (примитивы и объекты, созданные другими выражениями). Выражение (А-В) п(Си£>) будет представлено в графической системе деревом, показанным на рис. 8.23. Для обхода такого дерева и вычисления выражения используется метод обратного (post-order) обхода. Суть его состоит в том, что дерево обрабатывается рекурсивно - сначала левое поддерево, исходящее из узла, а потом правое поддерево, исходящее из узла. Результаты обработки каждого поддерева используются в качестве операндов при выполнении операции (как правило, двухместной), специфицированной в самом узле.
Изображение моделей, созданных с помощью конструктивной геометрии тел, формируется, как правило, с помощью метода трассировки лучей (см. упр. 8.10).
Читатель вправе задать вопрос, а чем же кардинально отличается полигональное представление объекта от представления такого же по форме объекта в рамках конструктивной геометрии тел? Отличие- в представлении объема объекта. При полигональном представлении объем, как таковой, не существует. Существуют только участки поверхностей, которые могут ограничивать какой-то объем, но, в принципе, это совсем не обязательно. В конструктивной геометрии тел существуют
