2В этой модели не показано неподвижное основание, относительно которого вращается первое звено. - Прим. ред.
8.3. Модель руки робота поворота в сочленении измеряется относительно собственного фрейма каждого звена. Первое звено - тело робота - поворачивается на угол 8 относительно вертикальной оси своего фрейма, а угол измеряется от оси х до некоторой фиксированной точки на нижней плоскости первого звена. Второе звено - плечо робота - связано с телом сочленением, позволяющим ему наклоняться в плоскости 2 = 0 фрейма плеча на угол ф, который измеряется от оси х этого же фрейма. Третье звено - предплечье - связано аналогичным сочленением с плечом и может наклоняться относительно плеча на угол \|/, измеряемый также в его собственном фрейме. Изменение углов в сочленениях приводит к перемещению фреймов плеча и предплечья относительно фрейма тела робота. Управляя этими тремя углами, можно перемещать конечную точку предплечья (на которой в реальном роботе закрепляется кисть со схватом) в трехмерном пространстве.
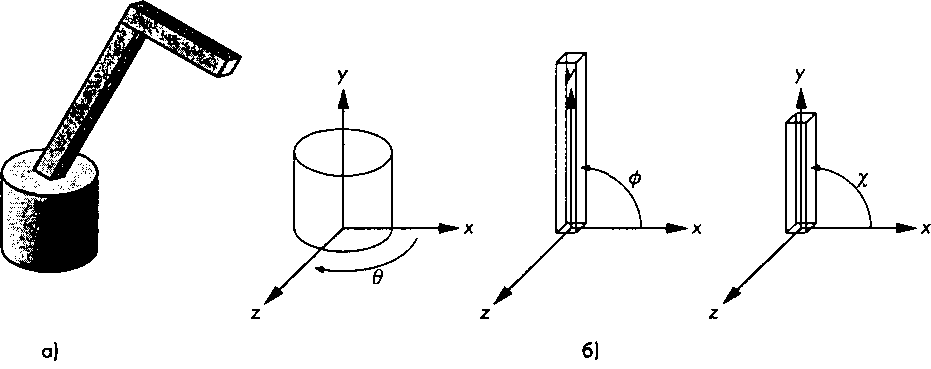
Рис. 8.8. Рука робота: а - составная модель; б - компоненты
Перед нами стоит задача разработать программу, которая будет формировать динамическое изображение движущегося робота. Вместо того чтобы независимо друг от друга описывать каждый элемент робота и его движение, мы воспользуемся подходом, основанным на суперпозиции движения отдельных звеньев. Тело робота может поворачиваться вокруг оси у собственного фрейма на угол 9. Следовательно, можно описать перемещение любой точки р на теле робота, воспользовавшись матрицей преобразования поворота R,(6).
Плечо робота поворачивается вокруг оси z собственного фрейма, но этот фрейм нужно привязать к центру верхней плоскости тела робота. Это можно сделать с помощью матрицы преобразования сдвига Т(0, Ии 0), где И\ - высота тела относительно плоскости основания. Именно в этой точке находится сочленение между первым и вторым звеньями. Но если поворачивается тело робота, то вместе с ним поворачивается и плечо, точнее фрейм плеча. Следовательно, в дополнение к преобразованию сдвига нужно применить и преобразование поворота, воспользовавшись матрицей R,(6). Таким образом, положение любой точки на втором звене, в том числе и вершин многогранника, представляющего параллелепипед, в процессе изменения углов в первом и втором сочленениях будет зависеть от произведения матриц R,.(e)T(0, А,, 0)К_.(ф). Матрицу К/ЭЩО, hu 0) можно рассматривать как матрицу преобразования фрейма плеча относительно мирового фрейма, а матрицу К-(ф) как матрицу положения плеча относительно тела робота (рис. 8.9).
