7.10. Растровое преобразование многоугольников
mytess = gluNewTess();
gluTessBeginPolygon(mytess, NULL); gluTessBeginContour(mytess); for(i=0;i<nvertices;i++)
glTessVertex(mytess, vertex[i], vertex[i]); gluTessEndContour(); gluTessEndPolygon(mytess);Основная идея использования имеющихся в OpenGL средств разбиения состоит в том, что от прикладной программы требуется описать контур исходного многоугольника, a OpenGL самостоятельно сформирует его составные части и выполнит их заполнение в соответствии с заданными параметрами.
В алгоритмах разбиения, реализованных в OpenGL, используется описанный выше тест охватывания и формируемый в нем параметр W. В зависимости от того, как точка внутри многоугольника охватывается описанным контуром, OpenGL по-разному заполняет области внутри многоугольника при заданных параметрах разбиения (рис. 7.49). В приведенном в конце главы обзоре литературы читатель встретит указания на источники, в которых анализируются различные варианты алгоритмов разбиения. Что касается пользователей OpenGL, то для них обращение к имеющимся в этой системе средствам разбиения гарантирует, что все дальнейшие операции будут совершаться только над выпуклыми плоскими многоугольниками.
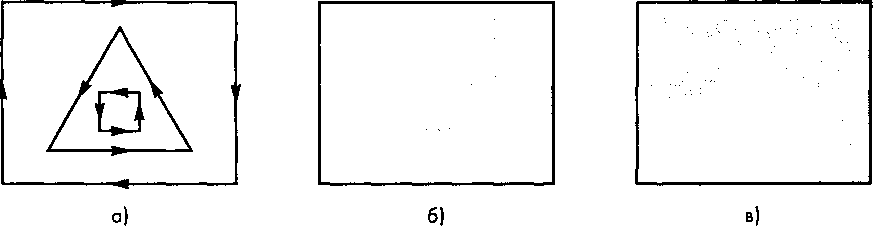
Рис. 7.49. Разбиение многоугольника: а - направление обхода контуров; б и в - варианты разбиения
7.10.3. Растровое преобразование с использованием г-буфера Теперь сведем воедино все, что было сказано в предыдущих разделах и главах об отображении многоугольников. Проследим, что происходит с многоугольником по мере его продвижения по конвейеру обработки. Сначала вершины и нормаль к плоскости многоугольника подвергаются геометрическим преобразованиям. На этом этапе не принимается во внимание, что вершины описывают именно многоугольник, - они обрабатываются как несвязанные геометрические объекты. При выполнении отсечения вершины уже связываются в многоугольник. Если многоугольник не отбрасывается в результате отсечения, он передается в модуль закрашивания и удаления невидимых поверхностей. На этой стадии, несмотря на выполнение нормализации проецирования, информация о глубине сохраняется. Если желательно использовать метод интерполяционного закрашивания, этой информации достаточно, чтобы вычислить освещенность каждой вершины многоугольника.
