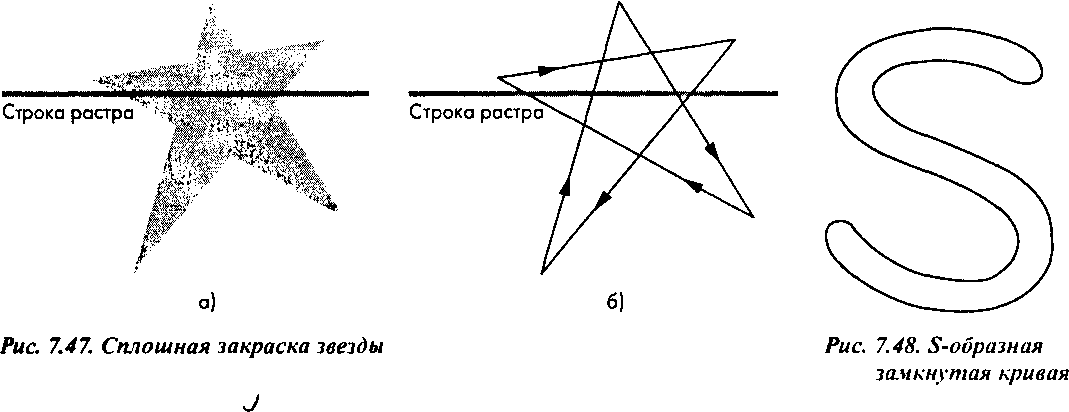
контура, причем оборот в направлении хода часовой стрелки учитывается положительным приращением значения IV, а против часовой стрелки - отрицательным. На рис. 7.47 пока зано, как будет обходиться контур звезды при тестировании точки р. Если тестируемая точка находится вне многоугольника, зондирующий луч не совершит ни одного полного оборота вокруг нее при обходе контура многоугольника и для этой точки И/= 0. Для тех точек внутри лучей звезды, которые залиты на рис. 7.46, IV = 1, а для точки р на рис. 7.47,6 IV =2. Таким образом, если считать внутренними точками многоугольника все точки, для которых IV > 0, то получим закраску, как на рис. 7.47,а.
При определении значения IV возникает ряд проблем. Рассмотрим 8-образную замкнутую кривую на рис. 7.48, которую можно аппроксимировать многоугольником со множеством вершин. Не совсем ясно, как в этом случае определить "обматывание" для точек, расположенных внутри кривой. Можно модифицировать сформулированное ранее определение четности-нечетности, распространить его на количество оборотов и получить таким образом приемлемый способ измерения значения IV ддя произвольной точки. Рассмотрим произвольную прямую (зондирующую прямую), проходящую через внутреннюю точку р, как показано на рис. 7.47,6, причем эта прямая не должна быть параллельна ни одному из ребер многоугольника. Значение параметра IV для этой точки равно количеству ребер, которые пересекают зондирующую прямую в направлении сверху вниз, минус количество ребер, которые пересекают ее в направлении снизу вверх. Если IV не равно 0, то точка лежит внутри многоугольника. Обращаю ваше внимание на то, что для этого теста не имеет значения, что считается низом, а что верхом.
7.10.2. Обработка многоугольников общего вида в OpenGL
OpenGL гарантирует корректное отображение только выпуклых многоугольников, а потому для отображения многоугольников общего вида приходится изобретать различные искусственные приемы. Один из подходов заключается в том, что прикладная программа должна самостоятельно следить за тем, чтобы все многоугольники в сцене удовлетворяли этому ограничению. Другой подход - разбить (tessellate) многоугольник общего вида на плоские выпуклые многоугольники, как правило, треугольники. Существует множество методов выполнения такого разбиения. Хорошим считается метод, который формирует не слишком длинные и узкие треугольники. Кроме того, желательно, чтобы после разбиения многоугольник можно было представить одним из составных примитивов, имеющихся в графической системе. В OpenGL для этого используются примитивы типа полоса из треугольников (triangle strips) и розетка из треугольников (triangle fans). Функция разбиения включена в состав библиотеки GLU. При обработке многоугольника без отверстий сначала создается новый объект разбиения (tessellator object), и в него передаются вершины исходного многоугольника:
