5.7. Матрицы параллельного проецирования Те матрицы проективного преобразования, которые формируются и используются в OpenGL, не так просты, как рассмотренные в разделе 5.3. В этом и следующем разделах мы подробно рассмотрим особенности формирования матриц проективного преобразования в OpenGL. Поскольку моделирование проецирования является ключевой проблемой в трехмерной компьютерной графике, без глубокого понимания используемых при этом математических методов нельзя ни написать хорошую прикладную программу, ни разработать новую графическую систему. Более того, хотя функции работы с проективными преобразованиями, которые имеются в OpenGL, и дают вполне удовлетворительные результаты в большинстве ситуаций, возникающих в практике разработки графических приложений, некоторые виды проекций, в частности косоугольные, непосредственно в OpenGL не поддерживаются. Если в приложении нужно организовать именно такую проекцию, приходится прибегать к косвенным методам, а для этого необходимо глубокое понимание механизмов работы системы. Ниже будет показано, как это знание может быть использовано на практике.
5.7.1. Нормализация проецирования Используемый в OpenGL подход базируется на методике нормализации проецирования (projection normalization), которая предусматривает сведение всех типов проекций к ортогональной, для чего выполняется предварительное искажение исходных объектов (рис. 5.30). Поскольку такое искажение может быть представлено в виде преобразования в однородных координатах, можно не выполнять фактическое искажение формы объектов, а добавить соответствующие матрицы преобразований к матрице обычного ортогонального проецирования и получить матрицу требуемого проективного преобразования, как показано схематически на рис. 5.31.
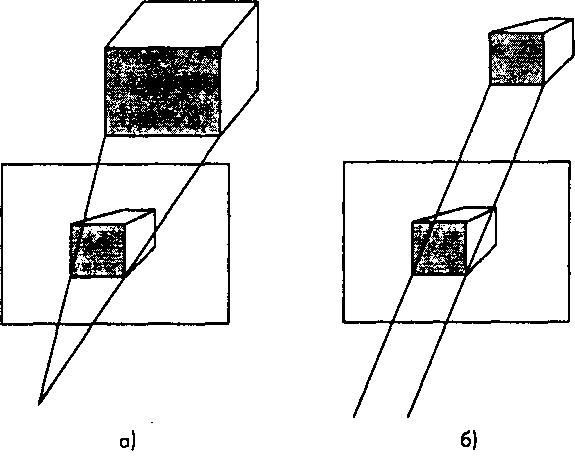
Рис 5.30. Предварительное искажение объекта: а - перспективная проекция; б - ортогональная проекция искаженного объекта
Визуализация
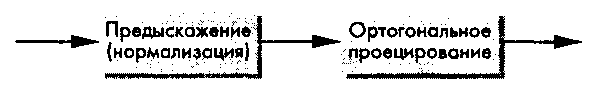
Рис 5.31. Нормализация преобразования
5.7.2. Матрицы ортогонального проективного преобразования Хотя параллельная проекция является частным случаем перспективной проекции, мы начнем с параллельной ортогональной проекции, а затем распространим методику нормализации на перспективную. Выше было показано, что проективное преобразование отображает точки трехмерного пространства на точки картинной плоскости и что такое преобразование является вырожденным (т.е. определитель матрицы преобразования равен 0). Все точки, расположенные на одном проецирующем луче, преобразуются в единственную точку на картинной плоскости.
