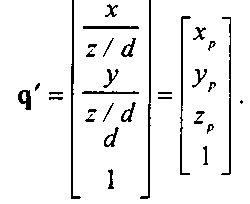
Итак, вы убедились, что, по крайней мере, простые перспективные преобразования можно реализовать в матричной форме, определив соответствующую 4х4-матрицу. Это преобразование выполняется после преобразования вида, заданного матрицей вида. Но в конце процесса нужно выполнить перспективное деление {perspective division), которое можно также реализовать в виде одной из стадий конвейерного процесса обработки (рис. 5.22).
5.3.2. Ортогональная проекция Ортогональная проекция - это частный случай параллельной проекции, при которой проецирующие лучи ортогональны картинной плоскости. Можно с определенной точностью считать, что ортогональная проекция получается в камере, имеющей объектив с очень большим фокусным расстоянием, причем картинная плоскость камеры ортогональна оптической оси ее объектива. Однако уравнения ортогонального проецирования можно вывести и непосредственно, не прибегая к "переносу" в бесконечность центра проецирования математической модели. На рис. 5.23 показана ортогональная проекция на картинную плоскость 2 = 0. При проецировании точки на эту плоскость сохраняются значения ее компонентов х и у, а уравнения проецирования будут иметь вид хР=х, ур=у, 1Р=0.
Запишем результат в виде матрицы преобразования однородных координат:
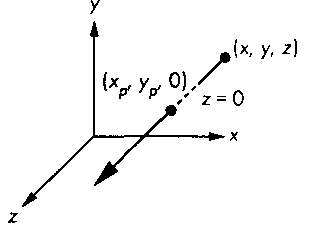
Рис. 5.23. Ортогональное проецирование
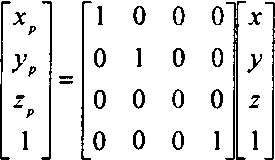
При выполнении ортогонального проективного преобразования отпадает необходимость в делении, хотя для обоих видов проективного преобразования можно использовать одну и ту же аппаратную реализацию конвейерной обработки.
Результаты, полученные для простых случаев, можно расширить на перспективное и параллельное проецирование общего вида, дополнив их последовательностью преобразований сдвига и поворота. Но сначала рассмотрим, как реализуется описанный математический аппарат в OpenGL.
5.3. Проецирование

5.4. Проективные преобразования в OpenGL
Рассматривая в разделе 5.3 процесс проецирования, мы не принимали во внимание характеристики камеры - фокусное расстояние объектива и размеры пленки (окна на картинной плоскости). На рис. 5.24 показан геометрический смысл _угл<г зрения (angle of view) для камеры-обскуры, которую мы рассматривали в главе 1. На изображении появляются только те объекты, которые попали внутрь угла зрения. Если окно на картинной плоскости имеет вид прямоугольника, то на изображении появятся только те объекты, которые окажутся внутри бесконечной пирамиды с вершиной в центре проецирования. Эта пирамида ограничивает зону видимости (view volume). Объекты, не попавшие в эту зону, отсекаются (clipped) и не включаются в отображаемую сцену. Таким образом, приведенное выше математическое описание процесса визуализации является неполным, поскольку мы не включили в него отсечение.
